
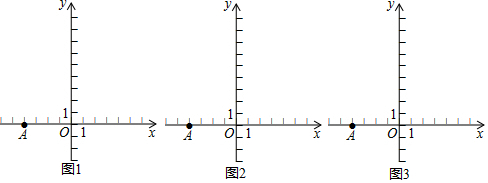
分析 (1)如图,作CD⊥y轴于D.先证明△ABO≌△BCD,推出BO=CD=b,OA=BD=4,推出OD=4+b,由此即可解决问题.
(2)①因为C(-b,4+b),所以点C在直线y=x+4上,图中的线段C1C2即为点C的运动轨迹.
②点C的运动轨迹是线段C1C2,线段的两个端点的坐标C2(-5,9),C1(2,2).
③先求出∠DGC=45°,进而得出C1,C2的坐标即可.
解答 解:(1)如图1,作CD⊥y轴于点D.
由题意可得AB=BC,∠ABC=90°,
∴∠DBC+∠OBA=90°.
∵∠AOB=∠BDC=90°,
∴∠OAB+∠OBA=90°.
∴∠OAB=∠DBC.
∴△OAB≌△DBC.
∴OB=DC,OA=DB.
∵点A的坐标为(-4,0),点B的坐标为(0,b),点B在y轴的正半轴上,
∴OA=4,OB=b.
∴OD=OB+BD=b+4,CD=OB=b.
由题意知点C在第二象限,
∴点C的坐标为(-b,b+4).
(2)①画图如图2.
②线段C1C2,其中C1,C2两点的坐标分别为C1(2,2),C2(-5,9),
线段C1C2所在直线与y轴所夹的锐角为45°.
③简要证明过程:如图3,
设点G的坐标为G(0,4),点H的坐标为H(4,0),可
得∠OGH=45°.
任取满足题意的点B(0,b)(其中-2≤b≤5),作出相应的线段BC和线段AC,作CD⊥y轴于点D.
由点G(0,4)可得OG=4=OA.
同(1)可得OB=CD,AO=BD.
所以 CD=OB=OD-BD=OD-OA=OD-OG=DG.
由CD⊥y轴于点D可得∠DGC=45°.
所以无论点B在y轴上如何运动,相应的点C在运动时总落在直线GH上.
而点B在y轴上运动满足-2≤b≤5时,
此时点C运动的路径是这条直线上的一部分,是线段C1C3(见图2),
其中与点B1(0,-2)对应的端点为C1(2,2);与点B2(0,5)对应的端点为C2(-5,9).
点评 本题考查作图旋转变换、轨迹、一次函数等知识,解题的关键是发现点C的坐标满足直线y=x+4,由此判断出点C的运动轨迹是线段,本题比较难,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
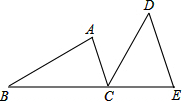 如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-3 | B. | m=1 | C. | m=1或m=-3 | D. | m≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小林在一块长为6m,宽为4m,一边靠墙的矩形小花园ABCD周围栽种了一种花来装饰,这种花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗?
如图所示,小林在一块长为6m,宽为4m,一边靠墙的矩形小花园ABCD周围栽种了一种花来装饰,这种花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com