
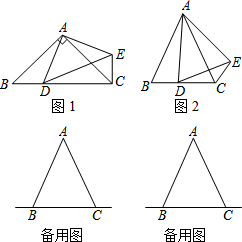
 已知:在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
已知:在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
|
|
|
|


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
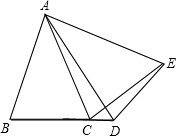
 如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.
如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.查看答案和解析>>
科目:初中数学 来源: 题型:
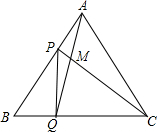 如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第
如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第| 4 |
| 3 |
| 8 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、这个地区从现在开始经过6至7天会发生降水 |
| B、这个地区未来10天内将会发生一次降水 |
| C、这个地区未来10天内发生降水比不发生降水的可能性大 |
| D、我们不能判断何时会有降水发生 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com