
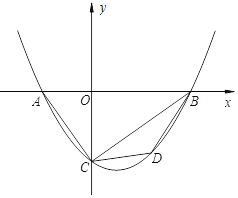
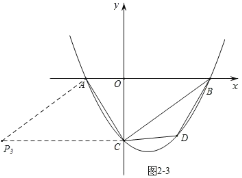
【题目】如图,抛物线y=a(x+2)(x﹣4)与x轴交于A,B两点,与y轴交于点C,且∠ACO=∠CBO.
(1)求线段OC的长度;
(2)若点D在第四象限的抛物线上,连接BD、CD,求△BCD的面积的最大值;
(3)若点P在平面内,当以点A、C、B、P为顶点的四边形是平行四边形时,直接写出点P的坐标.
【答案】(1)2![]() ;(2)2
;(2)2![]() ;(3)(2,2
;(3)(2,2![]() ),(6,﹣2
),(6,﹣2![]() )或(﹣6,﹣2
)或(﹣6,﹣2![]() )
)
【解析】
(1)由抛物线的解析式先求出点A,B的坐标,再证△AOC∽△COB,利用相似三角形的性质可求出CO的长;
(2)先求出抛物线的解析式,再设出点D的坐标(m,![]() m2﹣
m2﹣![]() m﹣2
m﹣2![]() ),用含m的代数式表示出△BCD的面积,利用函数的性质求出其最大值;
),用含m的代数式表示出△BCD的面积,利用函数的性质求出其最大值;
(3)分类讨论,分三种情况由平移规律可轻松求出点P的三个坐标.
(1)在抛物线y=a(x+2)(x﹣4)中,
当y=0时,x1=﹣2,x2=4,
∴A(﹣2,0),B(4,0),
∴AO=2,BO=4,
∵∠ACO=∠CBO,∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴![]() ,即
,即![]() ,
,
∴CO=2![]() ;
;
(2)由(1)知,CO=2![]() ,
,
∴C(0,﹣2![]() )
)
将C(0,﹣2![]() )代入y=a(x+2)(x﹣4),
)代入y=a(x+2)(x﹣4),
得,a=![]() ,
,
∴抛物线解析式为:y=![]() x2﹣
x2﹣![]() x﹣2
x﹣2![]() ,
,
如图1,连接OD,
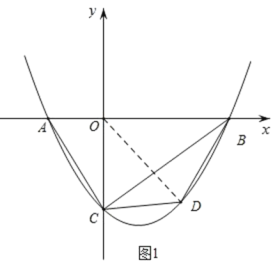
设D(m,![]() m2﹣
m2﹣![]() m﹣2
m﹣2![]() ),
),
则S△BCD=S△OCD+S△OBD﹣S△BOC
=![]() ×2
×2![]() m+
m+![]() ×4(﹣
×4(﹣![]() m2+
m2+![]() m+2
m+2![]() )﹣
)﹣![]() ×4×2
×4×2![]()
=﹣![]() m2+2
m2+2![]() m
m
=﹣![]() (m﹣2)2+2
(m﹣2)2+2![]() ,
,
根据二次函数的图象及性质可知,当m=2时,△BCD的面积有最大值2![]() ;
;
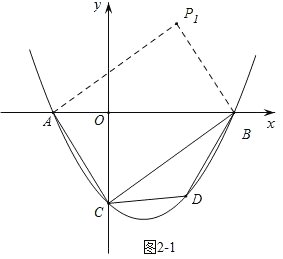
(3)如图2﹣1,当四边形ACBP为平行四边形时,由平移规律可知,点C向右平移4个单位长度,再向上平移2![]() 个单位长度得到点B,所以点A向右平移4个单位长度,再向上平移2
个单位长度得到点B,所以点A向右平移4个单位长度,再向上平移2![]() 个单位长度得到点P,因为A(﹣2,0),所以P1(2,2
个单位长度得到点P,因为A(﹣2,0),所以P1(2,2![]() );
);
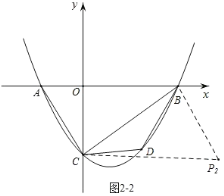
同理,在图2﹣2,图2﹣3中,可由平移规律可得P2(6,﹣2![]() ),P3(﹣6,﹣2
),P3(﹣6,﹣2![]() );
);
综上所述,当以点A、C、B、P为顶点的四边形是平行四边形时,点P的坐标为(2,2![]() ),(6,﹣2
),(6,﹣2![]() ),P3(﹣6,﹣2
),P3(﹣6,﹣2![]() ).
).


科目:初中数学 来源: 题型:
【题目】某校九年级有600名学生,在体育中考前进行了一次模拟体测.从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
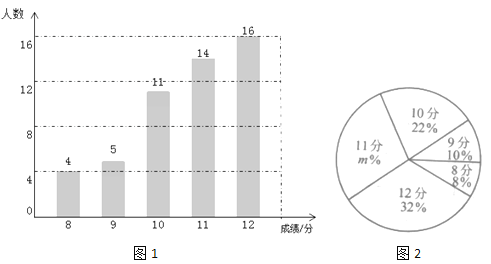
(Ⅰ)本次抽取到的学生人数为 ,图2中![]() 的值为 ;
的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和2015年我省财政收入分别为a亿元和b亿元,则a、b之间满足的关系式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
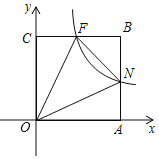
【题目】如图所示,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,双曲线y=kx﹣1(k≠0,x>0)与边AB、BC分别交于点N、F,连接ON、OF、NF.若∠NOF=45°,NF=2,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
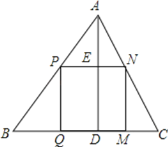
【题目】用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;乙同学说:“当正方形的一边在最短边上时,剪出的内接正方形最大”;丙同学说:“不确定,剪不出这样的正方形纸.”你认为谁说的有道理,请证明.(假设图中△ABC的三边a,b,c,且a>b>c,三边上的高分别记为ha,hb,hc)
查看答案和解析>>
科目:初中数学 来源: 题型:
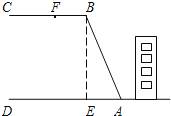
【题目】某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,斜坡AB的坡比为i=12:5,为了减缓坡面防山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.
(1)求改造前坡顶到地面的距离BE的长;
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(tan48.8°≈1.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现问题)
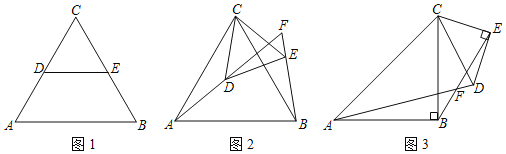
(1)如图1,已知△CAB和△CDE均为等边三角形,D在AC上,E在CB上,易得线段AD和BE的数量关系是 .
(2)将图1中的△CDE绕点C旋转到图2的位置,直线AD和直线BE交于点F.
①判断线段AD和BE的数量关系,并证明你的结论;
②图2中∠AFB的度数是 .
(探究拓展)
(3)如图3,若△CAB和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F,分别写出∠AFB的度数,线段AD、BE间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
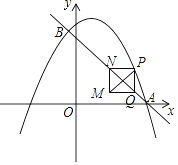
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com