
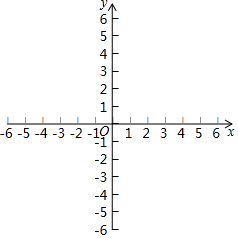 观察:点…A(-5,-2)、B(-4,-1),C(1,4)、D(2,5)、E(x,y)…;
观察:点…A(-5,-2)、B(-4,-1),C(1,4)、D(2,5)、E(x,y)…;分析 (1)将已知点在坐标系中描出可知位于同一直线上,利用待定系数法求解可得;
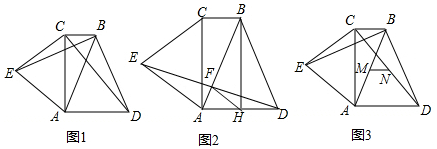
(2)求得直线MN的解析式可知MN∥AC,从而知△AMN和△CMN共底、等高,即可得证.
解答 解:(1)将A、B、C、D在坐标系中标出来,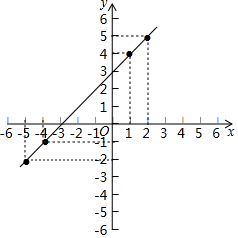
由图象可知,这些点都位于一条直线上,
设直线解析式为y=kx+b,
将A(-5,-2)、B(-4,-1)代入,得:
$\left\{\begin{array}{l}{-5k+b=-2}\\{-4k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴y=x+3;
(2)设M、N所在直线解析式为y=ax+b,
则$\left\{\begin{array}{l}{ma+b=0}\\{b=-m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-m}\end{array}\right.$,
∴直线MN解析式为y=x-m,
∵直线AC解析式为y=x+3,
∴AC∥MN,
∴△AMN和△CMN共底、等高,
∴S△AMN=S△CMN.
点评 本题主要考查坐标与图形的性质,熟练掌握待定系数法求函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,有一只蜗牛从直角坐标系的原点O向y轴正方向爬行,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,…当它走到点P(n,n)时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,…最后回到x轴上,则蜗牛所走过的路程s为4n-1厘米.
如图所示,有一只蜗牛从直角坐标系的原点O向y轴正方向爬行,它前进1厘米后,右转90°,再前进1厘米后,左转90°,再前进1厘米后,右转90°,…当它走到点P(n,n)时,左边碰到障碍物,就直行1厘米,再右转90°,前进1厘米,再左转90°,前进1厘米,…最后回到x轴上,则蜗牛所走过的路程s为4n-1厘米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 解决问题:如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是10$\sqrt{2}$+8.
解决问题:如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是10$\sqrt{2}$+8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一条船从灯塔C南偏东42°的A处出发,以每小时8海里的速度向正北航行到达B处,灯塔C在B的北偏西84°方向且距离B处16海里,则船从A到B航行了2小时.
如图,一条船从灯塔C南偏东42°的A处出发,以每小时8海里的速度向正北航行到达B处,灯塔C在B的北偏西84°方向且距离B处16海里,则船从A到B航行了2小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com