
分析 由100×30°=8×360°+120°可得点A100在第三象限,与x轴的正半轴成120°角,过点A100作AH⊥x轴于H,根据三角形外角的性质可得∠HA100O=30°,然后根据30°所对的直角边等于斜边的一半可求出OH,然后根据勾股定理可求出A100H,结合点A100所在的象限就可求出点A100的坐标.
解答 解:由100×30°=8×360°+120°可得,
点A100在第三象限,
此时∠A100OB=120°.
过点A作AH⊥x轴于H,
在Rt△AHO中,∠HAO=120°-90°=30°,
∴HO=$\frac{1}{2}$AO=$\frac{1}{2}$×4=2,
∴AH=$\sqrt{O{A}^{2}-O{H}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴A100的坐标是(-2,-2$\sqrt{3}$).
故答案为(-2,-2$\sqrt{3}$).
点评 本题考查了坐标与图形的变化、三角形外角的性质、30°所对的直角边等于斜边的一半、勾股定理等知识,需要注意的是根据相关线段的长度写点的坐标时,要根据点所在的象限确定纵横坐标的符号.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段CD、CB分别与⊙O相切于D、B两点,线段CD的延长线与直径BE的延长线交于点A,连接DE.
如图,已知线段CD、CB分别与⊙O相切于D、B两点,线段CD的延长线与直径BE的延长线交于点A,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
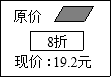 如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
如图是某超市中“飘柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )| A. | 15.36元 | B. | 16元 | C. | 24元 | D. | 23.04元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com