
【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
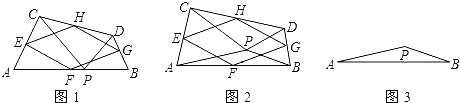
【答案】(1)四边形EFGH是菱形;
(2)成立,理由见解析;
(3)补全图形见解析;四边形EFGH是正方形,理由见解析.
【解析】试题分析:(1)连接AD、BC,利用SAS可判定△APD≌△CPB,从而得到AD=BC,因为EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线,则可以得到EF=FG=GH=EH,根据四边都相等的四边形是菱形,可推出四边形EFGH是菱形;(2)成立,可以根据四边都相等的四边形是菱形判定;(3)先将图形补充完整,再通过角之间的关系得到∠EHG=90°,已证四边形EFGH是菱形,则四边形EFGH是正方形.
试题解析:(1)四边形EFGH是菱形.
(2)成立.理由:连接AD,BC.
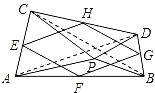
∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD.
即∠APD=∠CPB.
又∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS)
∴AD=CB.
∵E、F、G、H分别是AC、AB、BD、CD的中点,
∴EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线.
∴EF=![]() BC,FG=
BC,FG=![]() AD,GH=
AD,GH=![]() BC,EH=
BC,EH=![]() AD.
AD.
∴EF=FG=GH=EH.
∴四边形EFGH是菱形.
(3)补全图形,如答图.
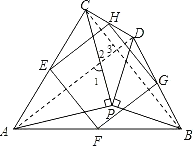
判断四边形EFGH是正方形.
理由:连接AD,BC.
∵(2)中已证△APD≌△CPB.
∴∠PAD=∠PCB.
∵∠APC=90°,
∴∠PAD+∠1=90°.
又∵∠1=∠2.
∴∠PCB+∠2=90°.
∴∠3=90°.
∵(2)中已证GH,EH分别是△BCD,△ACD的中位线,
∴GH∥BC,EH∥AD.
∴∠EHG=90°.
又∵(2)中已证四边形EFGH是菱形,
∴菱形EFGH是正方形.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,2.5,﹣3观察数轴,B,C两点之间的距离为 ;
与点A的距离为3的点表示的数是 ;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;
若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M: ,N: ;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P: ,Q: (用含m,n的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣ ![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
(1)请用列表或画树状图的方法表示取出数字的所有结果;
(2)求正比例函数y=kx的图象经过第一、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
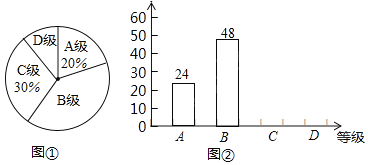
(1)在这次抽样调查中,共抽查了多少名学生?
(2)请在图②中把条形统计图补充完整;
(3)求出扇形统计图中“D级”部分所对应的扇形圆心角的大小;
(4)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(-22)+(-8)-(-5);(2)(-4![]() )-(-5
)-(-5![]() )+(-4
)+(-4![]() )-3
)-3![]() ;
;
(3)![]() ÷
÷![]() ; (4)-14+|3-5|-16÷(-2)×
; (4)-14+|3-5|-16÷(-2)×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.用等式表示第100个正方形点阵中的规律_________________.
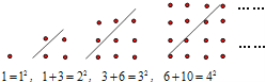
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a、b、c在数轴上的位置如图所示,则:
(1)用“<、>、=”填空:a____0,b____0,c_____0;
(2)用“<、>、=”填空:﹣a____0,a﹣b____0,c﹣a____0;
(3)化简:|﹣a|﹣|a﹣b|+|c﹣a|
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com