练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】阅读下列材料:让我们来规定一种运算： 。例如：

    按照这种运算的规定，请解答下列各个问题：

    （1）________，当x=______时，

    （2）求x，y的值，使（写出解题过程）

    【答案】（1）3x-2；；（2）y=2，x=8．

    【解析】

    (1)根据题中的新定义化简所求，计算即可得到结果；根据题中的新定义化简所求方程，求出方程的解即可得到x的值；
    (2)利用题中的新定义化简所求式子，计算即可确定出x与y的值．

    （1）原式=3x-2×1=3x-2；

    方程变形得：2x-（1-x）=0，
    去括号得：2x-1+x=0，
    移项合并得：3x=1，
    解得：x=；
    故答案为：.
    （2）根据题意得：，
    由②得：x=0.5y+7③，
    将③代入①得：0.75y+10.5-3-8y=-7，
    移项合并得：7.25y=14.5，
    解得：y=2，
    将y=2代入③得：x=8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在2019个“口”中依次填入一列数字m1，m2，m3；……. m2019，使得其中任意四个相邻的“口”中所填的数字之和都等于-10.已知m4=0，m6=-7，则m1+m2019的值为( )

    A.0B.-3C.-10D.-14

    查看答案和解析>>

    科目：初中数学 来源： 题型：

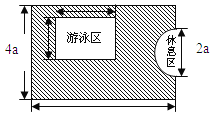
    【题目】如图，是一个长方形娱乐场所，其宽是4a米，长是6a米，现要求这个娱乐场拥有一半以上的绿地．小明提供了如图所示的设计方案，其中半圆形休息区和长方形游泳区以外的地方都是绿地，并且半圆形休息区的直径和长方形游泳区的宽都是2a米，游泳区的长3a米．

    （1）长方形娱乐场所的面积为　 　 平方米，

    休息区的面积为 　 　 平方米．

    （2）请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求？并说明理由．

    （3）若长方形娱乐场所的宽为80米，绿化草地每平方米需要费用20元，求小明设计方案中绿化草地的费用（π取3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知矩形ABCD的一条边AD=8，E是BC边上的一点，将矩形ABCD沿折痕AE折叠，使得顶点B落在CD边上的点P处，PC=4（如图1）．

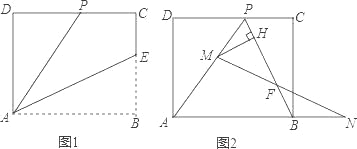
    （1）求AB的长；

    （2）擦去折痕AE，连结PB，设M是线段PA的一个动点（点M与点P、A不重合）．N是AB沿长线上的一个动点，并且满足PM=BN．过点M作MH⊥PB，垂足为H，连结MN交PB于点F（如图2）．

    ①若M是PA的中点，求MH的长；

    ②试问当点M、N在移动过程中，线段FH的长度是否发生变化？若变化，说明理由；若不变，求出线段FH的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数过点（－2，5），和直线，分别在下列条件下求这个一次函数的解析式.

    （1）它的图象与直线平行；

    （2）它的图象与y轴的交点和直线与y轴的交点关于轴对称.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：一辆汽车在一个十字路口遇到红灯刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA＝30°和∠DCB＝60°，如果斑马线的宽度是AB＝3米，驾驶员与车头的距离是0.8米，这时汽车车头与斑马线的距离x是多少？

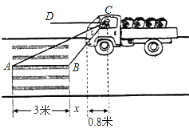
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：我们知道，，类似地，我们把看成一个整体，则.“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛.

    尝试应用：

    （1）把看成一个整体，合并的结果是______________.

    （2）当时，代数式的值为，则当时，求代数式的值.

    拓广探索：

    （3）已知，，，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点表示的数为，点表示的数为，动点从点出发以每秒个单位长度的速度沿负方向运动，动点从原点出发以每秒个单位长度的速度沿负方向运动，动点从点出发以每秒个单位的速度先沿正方向运动，到达原点后立即按原速反方向运动，三点同时出发，出发时间为（秒）．

    （1）点在数轴上所表示的数分别为：____________，____________；

    （2）当两点重合时，求此时点在数轴上所表示的数；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

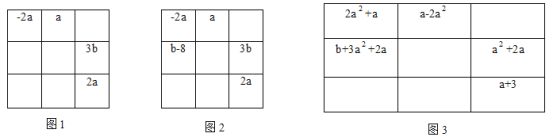
    【题目】在3×3的方格中，每行、每列及对角线上的3个代数式的和都相等，我们把这样的方格图叫做“等和格”。如图的“等和格”中，每行、每列及对角线上的3个代数式的和都等于15.

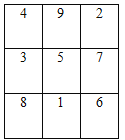
    （1）图1是显示部分代数式的“等和格”，可得a=_______（含b的代数式表示）；

    （2）图2是显示部分代数式的“等和格”，可得a=__________,b=__________;

    （3）图3是显示部分代数式的“等和格”，求b的值。（写出具体求解过程）

    查看答案和解析>>

    同步练习册答案