
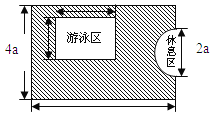
【题目】如图,是一个长方形娱乐场所,其宽是4a米,长是6a米,现要求这个娱乐场拥有一半以上的绿地.小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,并且半圆形休息区的直径和长方形游泳区的宽都是2a米,游泳区的长3a米.
(1)长方形娱乐场所的面积为 平方米,
休息区的面积为 平方米.
(2)请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求?并说明理由.
(3)若长方形娱乐场所的宽为80米,绿化草地每平方米需要费用20元,求小明设计方案中绿化草地的费用(π取3).
【答案】(1)24a2,![]() ;(2)他的设计方案符合要求,理由见解析;(3)小明设计方案中绿化草地的费用为132000元.
;(2)他的设计方案符合要求,理由见解析;(3)小明设计方案中绿化草地的费用为132000元.
【解析】
(1)根据长方形面积公式和半圆的面积求法列出代数式即可;
(2)求出休息区和游泳区的总面积,然后根据题意判断即可;
(3)根据题意,可以计算出a的值,然后根据绿化草地每平方米需要费用20元,即可求得小明设计方案中绿化草地的费用.
解:(1)由题意可得,
长方形娱乐场所的面积为:6a×4a=24a2,
休息区的面积为:![]() ,
,
故答案为:24a2,![]() ;
;
(2)他的设计方案符合要求,
理由:∵休息区和游泳区总面积为:3a×2a +![]() =6a2+
=6a2+![]() <
<![]() ×24a2,
×24a2,
∴他的设计方案符合要求;
(3)由题意可得,4a=80,解得,a=20,
∴绿化草地的费用为:[24a2(6a2+![]() )]×20=[24×202(6×202+
)]×20=[24×202(6×202+![]() )]×20=132000(元),
)]×20=132000(元),
答:小明设计方案中绿化草地的费用为132000元.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 75 | 75 | ||
乙 | 33.3 | 70 |
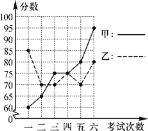
(1)请根据统计图填写上表:
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看,你得出什么结论;
②从折线图上两名同学分数的走势上看,你认为反映出什么问题?
查看答案和解析>>
科目:初中数学 来源: 题型:
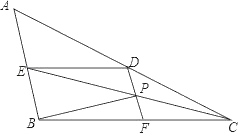
【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨),并将调查数据进行了如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
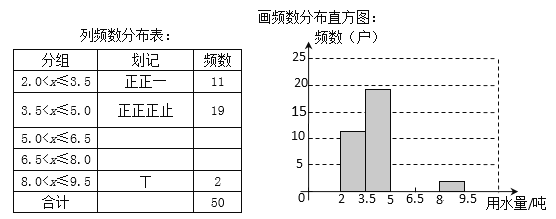
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1) 图中的点被线段隔开分成四层,第一层有1个点,第二层有3个点,第三层有5个点,第四层有___________个点;
(2) 如果要你继续画下去,那么第五层有________点, 第10层有_________点;
(3) 某一层上有77个点,你可知道这是第_________层;
(4) 第一层与第二层的和是__________,前三层的和是_________,前四层和为____________,
你有没有发现什么规律?
根据你的推测,前一百层的和是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:让我们来规定一种运算:![]() 。例如:
。例如:![]()
按照这种运算的规定,请解答下列各个问题:
(1)![]() ________,当x=______时,
________,当x=______时,![]()
(2)求x,y的值,使![]() (写出解题过程)
(写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
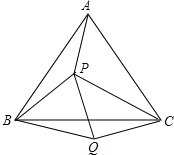
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com