
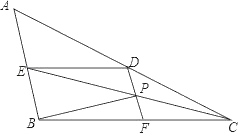
【题目】如图,在△ABC中,CE平分∠ACB交AB于E点,DE∥BC,DF∥AB.
(1)若∠BCE=25°,请求出∠ADE的度数;
(2)已知:BF=2BE,DF交CE于P点,连结BP,AB⊥BP.
①猜想:△CDF的边DF与CD的数量关系,并说明理由;
②取DE的中点N,连结NP.求证:∠ENP=3∠DPN.
【答案】(1)∠ADE=50°;(2)①CD=2DF;见解析;②见解析.
【解析】
(1)利用角平分线得出∠ACB=2∠BCE=50°,再利用两直线平行,同位角相等即可得出结论;
(2)先判断出四边形BEDF是平行四边形,进而得出DE=2DF,再利用角平分线及平行线得出DE=CD,即可得出结论;
(3)先利用倍长中线法得出NG=NP,∠EGN=∠DPN,再用直角三角形的中线得出∠EGN=∠EBN,再构造出菱形判断出∠BEN=∠BHN,即可得出结。
(1)∵CE平分∠ACB交AB于E点,
∴∠ACB=2∠BCE,
∵∠BCE=25°,
∴∠ACB=50°,
∵DE∥BC,
∴∠ADE=∠ACB=50°;
(2)①∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∴DE=BF,DF=BE,
∵BF=2BE,
∴DE=2DF,
∵CE平分∠ACB交AB于E点,
∴∠BCE=∠ACE,
∵DE∥BC,
∴∠DEC=∠BCE,
∴∠DEC=∠DCE,
∴CD=DE,
∵DE=2DF,
∴CD=2DF;
(3)如图,
延长PN交AB于G,
∵DF∥AB,
∴∠EGN=∠DPN,
∵∠ENG=∠DNP,
∵点N是DE中点,
∴EN=DN,
∴△ENG≌△DNP(AAS),
∴∠EGN=∠DPN,GN=PN,
∵AB⊥BP,
∴∠ABP=90°,
∴BN=GN,
∴∠EGN=∠EBN,
∵DE=2EN,DE=2BE,
∴EN=BE,
∴∠ENB=∠EBN=∠EGN=∠DPN,
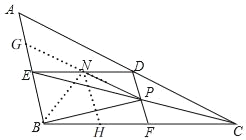
过点N作NH∥BE交BC于H,
∵BE∥DF,
∴NH∥DF,
∴∠PNH=∠DPN,
∵EN∥BH,NH∥BE,
∴四边形BENH是平行四边形,
∵BE=EN,
∴BENH是菱形,
∵BE是菱形对角线,
∴∠BNH=∠BNE=DPN,
∴∠ENP=∠BNE+∠BNH+∠PNH=∠DPN+∠DPN+∠DPN=3∠DPN.


科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条东西直大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向东方向为正,当天行驶情况记录如下(单位:千米):
+9, -5, +7, -14, +1, -10, +8;
(1)点A在岗亭的 边方向,距离岗亭 千米。
(2)若他离开岗亭超过10千米对讲机就会与岗亭值班员失联,请问他这一天有没有失联过?有几次?请说明理由。
(3)若摩托车每行驶100千米耗油6升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步改善环境,郑州市今年增加了绿色自行车的数量,已知A型号的自行车比B型号的自行车的单价低30元,买8辆A型号的自行车与买7辆B型号的自行车所花费用相同.
(1)A,B两种型号的自行车的单价分别是多少?
(2)若购买A,B两种自行车共600辆,且A型号自行车的数量不多于B型号自行车的一半,请你给出一种最省钱的方案,并求出该方案所需要的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
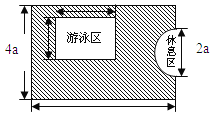
【题目】如图,是一个长方形娱乐场所,其宽是4a米,长是6a米,现要求这个娱乐场拥有一半以上的绿地.小明提供了如图所示的设计方案,其中半圆形休息区和长方形游泳区以外的地方都是绿地,并且半圆形休息区的直径和长方形游泳区的宽都是2a米,游泳区的长3a米.
(1)长方形娱乐场所的面积为 平方米,
休息区的面积为 平方米.
(2)请你判断他的设计方案是否符合娱乐场拥有一半以上的绿地的要求?并说明理由.
(3)若长方形娱乐场所的宽为80米,绿化草地每平方米需要费用20元,求小明设计方案中绿化草地的费用(π取3).
查看答案和解析>>
科目:初中数学 来源: 题型:
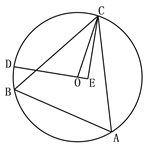
【题目】如图,△ABC为⊙O的内接三角形,BC=24 , ![]() ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 过点(-2,5),和直线
过点(-2,5),和直线![]() ,分别在下列条件下求这个一次函数的解析式.
,分别在下列条件下求这个一次函数的解析式.
(1)它的图象与直线![]() 平行;
平行;
(2)它的图象与y轴的交点和直线![]() 与y轴的交点关于
与y轴的交点关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
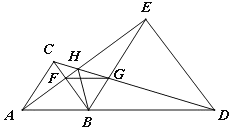
【题目】如图所示,已知△ABC和△BDE都是等边三角形。下列结论:① AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥ FG∥AD。其中正确的有_______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com