
【题目】联想三角形外心的概念,我们可引入如下概念:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.例:已知![]() ,则点
,则点![]() 为
为![]() 的准外心(如图
的准外心(如图![]() ).
).
![]() 如图
如图![]() ,
,![]() 为正三角形
为正三角形![]() 的高,准外心
的高,准外心![]() 在高
在高![]() 上,且
上,且![]() ,求
,求![]() 的度数.
的度数.
![]() 如图
如图![]() ,若
,若![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,![]() ,准外心
,准外心![]() 在
在![]() 边上,试探究
边上,试探究![]() 的长.
的长.



【答案】∠APB=90°;(2)PA=![]() 或6.
或6.
【解析】
(1)利用分类讨论:①若PB=PC,②若PA=PC,③若PA=PB,进而求出即可;
(2)利用分类讨论:①若PB=PA,②若PA=PC,③若PC=PB,进而求出即可.
(1)①若PB=PC,连结PB,则∠PCB=∠PBC.
∵CD为等边三角形的高.∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,∴PD=![]() DB=
DB=![]() AB.
AB.
与已知PD=![]() AB矛盾,∴PB≠PC.
AB矛盾,∴PB≠PC.
②若PA=PC,连结PA,
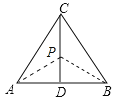
则∠PCA=∠PAC.
∵CD为等边三角形的高.∴AD=BD,∠PCA=30°,
∴∠PAD=∠PAC=30°,∴PD=![]() DA=
DA=![]() AB.
AB.
与已知PD=![]() AB矛盾,∴PA≠PC.
AB矛盾,∴PA≠PC.
③若PA=PB,由PD=![]() AB,得PD=BD,
AB,得PD=BD,
∴∠BPD=45°,
故∠APB=90°;
(2)①若PB=PA,设PA=x,
∵∠C=90°,AB=13,BC=5,
∴AC=12,则CP=12-x,
∴x2=(12-x)2+52,
∴解得:x=![]() ,即PA=
,即PA=![]() .
.
②若PA=PC,则PA=6.
③若PC=PB,由图知,
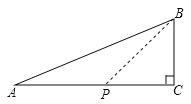
在Rt△PBC中,不可能,
故PA=![]() 或6.
或6.


科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.现有下列四个结论:①
的中点.现有下列四个结论:①![]() ;②四边形
;②四边形![]() 的面积等于
的面积等于![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数为( )
.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() 、
、![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 和
和![]() 交于点
交于点![]() ,有如下结论:①
,有如下结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ≌
≌![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() ;⑥
;⑥![]() ;⑦
;⑦![]() .其中不正确的结论的个数是( )
.其中不正确的结论的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )

A. 6 B. 9 C. 6![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
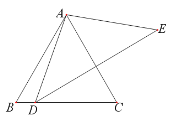
【题目】如图,△ABC是等边三角形,点D在BC上,△ADE是等腰三角形,AD =AE ,∠DAE =100°,当DE⊥AC时,求∠BAD和∠EDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线交于点
的对角线交于点![]() ,把边
,把边![]() 、
、![]() 分别绕点
分别绕点![]() 、
、![]() 同时逆时针旋转
同时逆时针旋转![]() 得四边形
得四边形![]() ,其对角线交点为
,其对角线交点为![]() ,连接
,连接![]() .下列结论:
.下列结论:
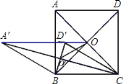
①四边形![]() 为菱形;
为菱形;
②![]() ;
;
③线段![]() 的长为
的长为![]() ;
;
④点![]() 运动到点
运动到点![]() 的路径是线段
的路径是线段![]() .其中正确的结论共有( )
.其中正确的结论共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com