
【题目】某年级共有330名男生,为了解该年级男生1000米跑步成绩(单位:分/秒)的情况,从中随机抽取30名男生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a.1000米跑步的频数分布表如下:
分组 | 3′17″<x≤3′ 37″ | 3′37″<x≤3′ 57″ | 3′ 57″<x≤4′ 17″ | 4′ 17″<x≤4′ 37″ | 4′ 37″<x≤4′ 57″ | 4′ 57″<x≤5′ 17″ |
频数 | 10 | 9 | m | 2 | 2 | 1 |
注:3′37″即3分37秒
b.1000米跑步在3′37″<x≤3′57″这一组是:
3′39 ″ 3′42 ″ 3′45 ″ 3′45″ 3′50 ″ 3′52 ″ 3′53″ 3′55″ 3′57″
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)根据表频数分布表画出相应的频数分布直方图.
(3)若男生1000米跑步成绩等于或者优于3′52″,成绩记为优秀.请估计全年级男生跑步成绩达到优秀的人数.
【答案】(1)6;(2)见解析;(3)115.
【解析】
(1)用样本容量30减去其他各成绩段的频数得到跑步时间为3′ 57″<x≤4′ 17″的频数m的值;
(2)根据频数分布表画出频数分布直方图即可
(3)先计算样本中男生1000米跑步成绩等于或者优于3′52″的百分比,再用全年级男生人数乘以这个百分比即可求解.
解:(1)m=30-10-9-2-2-1=6;
(2)由频数分布表得到频数分布直方图如图所示:

(3)由表格及1000米跑步在3′37″<x≤3′57″中的具体数据可得:男生1000米跑步成绩等于或者优于3′52″的频数为15.故估计全年级男生跑步成绩达到优秀的人数为:330×![]() =115人
=115人


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图. 
(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
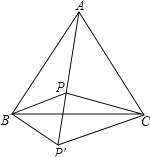
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )
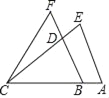
A. 1:1 B. 2:1 C. 1:2 D. 2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)写出数轴上点A表示的数;
(2)将长方形OABC沿数轴向右水平移动,移动后的长方形记为![]() ,若移动后的长方形
,若移动后的长方形![]() 与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的
与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的![]() 时,写出数轴上点
时,写出数轴上点![]() 表示的数;
表示的数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1: ![]() ,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
A.10 ![]() 米
米
B.15米
C.20 ![]() 米
米
D.30米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com