
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图. 
(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
【答案】
(1)50
(2)解:根据题意得:
女生评级3A的学生是:50×16%﹣3=8﹣3=5(人),
女生评级4A的学生是:50×50%﹣10=25﹣10=15(人),
如图:

(3)解:根据题意如表:

∵共有12种等可能的结果数,其中一名男生和一名女生的共有7种,
∴P= ![]() ,
,
答:选中一名男生和一名女生的概率为: ![]()
【解析】解:因为合格的男生有2人,女生有1人,共计2+1=3人,
又因为评级合格的学生占6%,
所以全班共有:3÷6%=50(人).
故答案为:50.
(1)根据合格的男生有2人,女生有1人,得出合格的总人数,再根据评级合格的学生占6%,即可得出全班的人数;(2)根据折线统计图和扇形统计图以及全班的学生数,即可得出女生评级3A的学生和女生评级4A的学生数,即可补全折线统计图;(3)根据题意画出图表,再根据概率公式即可得出答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,且
,且![]() .连接
.连接![]() 交对角线
交对角线![]() 于
于![]() ,连接
,连接![]() .下列结论:
.下列结论:

①![]() ;②
;②![]() 为等边三角形;
为等边三角形;
③![]() ; ④
; ④![]() .其中结论正确的是
.其中结论正确的是
A.只有①② | B.只有①②④ |
C.只有③④ | D.①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
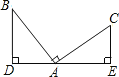
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论: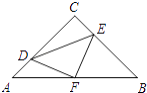
①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A.①②③
B.①④⑤
C.①③④
D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,连结CD,某抛物线y=ax2+bx+c(a≠0)经过点D、点E(1,1).
(1)若该抛物线过原点O,则a=;
(2)若点Q在抛物线上,且满足∠QOB与∠BCD互余,要使得符合条件的Q点的个数是4个,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+n.
(1)当销售单价x定为25元时,李明每月获得利润为w为1250元,则n=;
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?并求最大利润为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
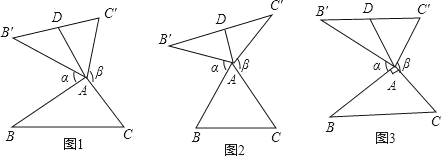
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有330名男生,为了解该年级男生1000米跑步成绩(单位:分/秒)的情况,从中随机抽取30名男生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a.1000米跑步的频数分布表如下:
分组 | 3′17″<x≤3′ 37″ | 3′37″<x≤3′ 57″ | 3′ 57″<x≤4′ 17″ | 4′ 17″<x≤4′ 37″ | 4′ 37″<x≤4′ 57″ | 4′ 57″<x≤5′ 17″ |
频数 | 10 | 9 | m | 2 | 2 | 1 |
注:3′37″即3分37秒
b.1000米跑步在3′37″<x≤3′57″这一组是:
3′39 ″ 3′42 ″ 3′45 ″ 3′45″ 3′50 ″ 3′52 ″ 3′53″ 3′55″ 3′57″
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)根据表频数分布表画出相应的频数分布直方图.
(3)若男生1000米跑步成绩等于或者优于3′52″,成绩记为优秀.请估计全年级男生跑步成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
小淇同学作法如下:
(1)在直线l上任意取一点C,连接AC;
(2)作AC的中点O;
(3)以O为圆心,OA长为半径画弧交直线l于点B,如图所示;
(4)作直线AB.
则直线AB就是所要作图形.
你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com