
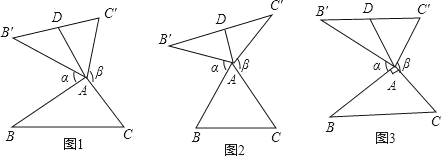
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
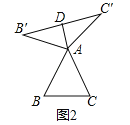
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
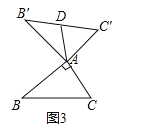
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
【答案】(1)①![]() ;②4;(2)AD=
;②4;(2)AD=![]() BC.
BC.
【解析】
(1)①首先证明△ADB'是含有30°的直角三角形,可得AD![]() AB'即可解决问题;
AB'即可解决问题;
②首先证明△BAC≌△B'AC',根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD![]() BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题.
BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题.
(1)①如图2中,∵△ABC是等边三角形,∴AB=BC=AC=AB'=AC'.
∵DB'=DC',∴AD⊥B'C'.
∵∠BAC=60°,∠BAC+∠B'AC'=180°,∴∠B'AC'=120°,∴∠B'=∠C'=30°,∴AD![]() AB'
AB'![]() BC.
BC.
故答案为:![]() .
.
②如图3中,∵∠BAC=90°,∠BAC+∠B'AC'=180°,∴∠B'AC'=∠BAC=90°.
∵AB=AB',AC=AC',∴△BAC≌△B'AC',∴BC=B'C'.
∵B'D=DC',∴AD![]() B'C'
B'C'![]() BC=4.
BC=4.
故答案为:4.
(2)结论:AD![]() BC.
BC.
理由:如图1中,延长AD到M,使得AD=DM,连接B'M,C'M.
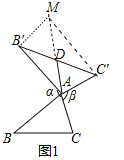
∵B'D=DC',AD=DM,∴四边形AC'MB'是平行四边形,∴AC'=B'M=AC.
∵∠BAC+∠B'AC'=180°,∠B'AC'+∠AB'M=180°,∴∠BAC=∠MB'A.
∵AB=AB',∴△BAC≌△AB'M,∴BC=AM,∴AD![]() BC.
BC.


科目:初中数学 来源: 题型:
【题目】小明爸爸装修要粉刷断居室的墙面,在家装商场选购某品牌的乳胶漆:
规格(升/桶) | 价格(元/桶) | |
大桶装 | 18 | 225 |
小桶装 | 5 | 90 |
小明爸估算家里的粉刷面积,若买“大桶装”,则需若干桶但还差2升;若买“小桶装”,则需多买11桶但会剩余1升,
(1)小明爸预计墙面的粉刷需要乳胶漆多少升?
(2)喜迎新年,商场进行促销:满1000减120元现金,并且该品牌商家对“小桶装”乳胶漆有“买4送1“的促销活动,小明爸打算购买“小桶装”,比促销前节省多少钱?
(3)在(2)的条件下,商家在这次乳胶漆的销售买卖中,仍可盈利25%,则小桶装乳胶漆每桶的成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图. 
(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
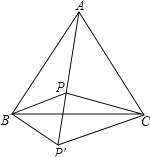
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
(1)求证:四边形AFCE是菱形.
(2)若AC=8,EF=6,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com