
【题目】某政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+n.
(1)当销售单价x定为25元时,李明每月获得利润为w为1250元,则n=;
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?并求最大利润为多少元.
【答案】
(1)500
(2)解:由题意,得:w=(x﹣20) ![]() y,
y,
=(x﹣20) ![]() (﹣10x+500)=﹣10x2+700x﹣10000,
(﹣10x+500)=﹣10x2+700x﹣10000,
令:﹣10x2+700x﹣10000=2000,
解这个方程得:x1=30,x2=40(舍).
答:李明想要每月获得2000元的利润,销售单价应定为30元
(3)解:由(2)知:w=﹣10x2+700x﹣10000,∴ ![]() .
.
∵﹣10<0,∴抛物线开口向下.
∵x≤32∴w随x的增大而增大.
∴当x=32时,w最大=2160.
答:销售单价定为32元时,每月可获得最大利润,最大利润为2160元
【解析】解:(1)∵y=﹣10x+n,当销售单价x定为25元时,李明每月获得利润为w为1250元,
∴则W=(25﹣20)×(﹣10×25+n)=1250,
解得:n=500;
故答案为:500.
(1)利润=销售量乘以每件的利润可求出;
(2)由利润=销售量乘以每件的利润(销售量y=-10x+n)得到w关于x的二次函数,再由w=2000得到关于x的一元二次方程,求解可得符合条件的x值;
(3)由(2)得到w关于x的二次函数,根据二次函数的性质可求出函数的定价和最值.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( )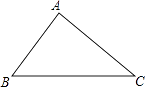
A.10﹣5 ![]()
B.5+5 ![]()
C.15﹣5 ![]()
D.15﹣10 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C2017 . 若点P是第2016段抛物线的顶点,则P点的坐标为 . 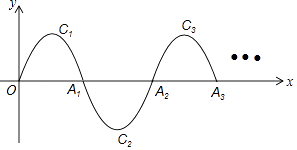
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图. 
(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知在数轴上有A、 B两点,点A表示的数是-6,点B表示的数是9.点P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从点B出发,以每秒3个单位的速度沿数轴负方向运动,当点Q到达点A时,两点同时停止运动,设运动时间为t秒.
(1) AB=____ ;当t=1时,点Q表示的数是___ ;当t=___时,P、Q两点相遇;
(2)如图2,若点M为线段AP的中点,点N为线段BP中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由.若不变,请求出线段MN的长;
(3)如图3,若点M为线段的AP中点,点T为线段BQ中点,则点M表示的数为______;点T表示的数为______;MT=______ (用含t的代数式填空).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )
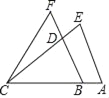
A. 1:1 B. 2:1 C. 1:2 D. 2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).
①以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1 .
②画出△ABC绕C点顺时针旋转90°后得到的△A2B2C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com