
【题目】已知抛物线:y=ax2+bx+c(a<0)经过A(2,4)、B(﹣1,1)两点,顶点坐标为(h,k),则下列正确结论的序号是( )
①b>1;②c>2;③h>![]() ;④k≤1.
;④k≤1.
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
【答案】B
【解析】分析:根据点A、B的坐标,利用待定系数法即可求出b=-a+1、c=-2a+2,结合a<0,可得出b>1、c>2,即结论①②正确;由抛物线顶点的横坐标h=-![]() ,可得出h=
,可得出h=![]() -
-![]() ,即h>
,即h>![]() ,结论③正确;由抛物线y=ax2+bx+c(a<0)经过A(-1,1),可得出k≥1,结论④错误.综上即可得出结论.
,结论③正确;由抛物线y=ax2+bx+c(a<0)经过A(-1,1),可得出k≥1,结论④错误.综上即可得出结论.
详解:∵抛物线过点A(﹣1,1),B(2,4),
∴![]() ,
,
∴b=﹣a+1,c=﹣2a+2.
∵a<0,
∴b>1,c>2,
∴结论①②正确;
∵抛物线的顶点坐标为(h,k),
∴h=﹣![]() =
=![]() -
-![]() ,
,
∵a<0
∴h>![]() ,结论③正确;
,结论③正确;
∵抛物线y=ax2+bx+c(a<0)经过A(﹣1,1),顶点坐标为(h,k),
∴k≥1,结论④不正确.
综上所述:正确的结论有①②③.
故选:B.


科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:

(1)分别求出表示甲、乙两同学登山过程中路程![]() (千米)与时间
(千米)与时间![]() (时)的函数解析式;(不要求写出自变量
(时)的函数解析式;(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)当甲到达山顶时,乙行进到山路上的某点![]() 处,求
处,求![]() 点距山顶的距离;
点距山顶的距离;
(3)在(2)的条件下,设乙同学从![]() 处继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点
处继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点![]() 处与乙相遇,此时点
处与乙相遇,此时点![]() 与山顶距离为1.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
与山顶距离为1.5千米,相遇后甲、乙各自按原来的路线下山和上山,求乙到达山顶时,甲离山脚的距离是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
利用图象法解一元二次不等式:x2-2x-3>0.
解:设y=x2-2x-3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.
又∵当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
(1)观察图象,直接写出一元二次不等式:x2-2x-3<0的解集是 ;
(2)仿照上例,用图象法解一元二次不等式:x2-1>0.(大致图象画在答题卡上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数-3,B点表示数b,C点表示数c,且b.c满足![]()
![]()
(1)b= ,c= .
(2)若使C.B两点的距离是A.B两点的距离的2倍,则需将点C向左移动 个单位长度.
(3)点A.B.C开始在数轴上运动,若点A以每秒m个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒;
①点A.B.C表示的数分别是 . . (用含m.t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当m为何值时,2d1-d2的值不会随着时间t的变化而改变,并求出此时2d1-d2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为50元/件的![]() 恤.经试销发现,销售量
恤.经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数关系,试销数据如下表:
(元/件)符合一次函数关系,试销数据如下表:
售价(元/件) | …… | 55 | 60 | 70 | …… |
销量(件) | …… | 75 | 70 | 60 | …… |
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价![]() 之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
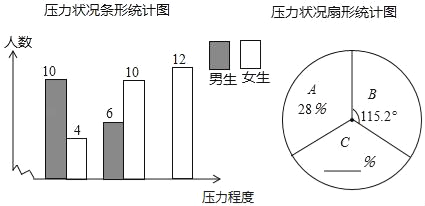
【题目】中考科目已经发生变革,继中考增加体育实验之后,从2019年开始河南中考开始增设生物和地理科目,针对于此学校教务处王老师负责调查学生对此变革是否有压力,设置问题答案如下(A:大,B:一般,C:无),再将调查结果制成两幅不完统计图(如图所示),请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图和扇形统计图补充完整;
(3)为了缓解学生压力,王老师从被调查的A类和B类学生中分别选取一名学生进行详细心理调查,请用合适的方法恰好选中一名男生和一名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
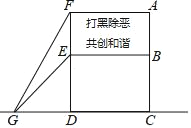
【题目】2018年年初,某小区应辖区派出所要求在广场树立一个“打黑除恶,共创和谐”的矩形电子灯牌,如图所示,施工人员在两侧加固合金框架,已知合金框架底端G距广告牌立柱距离FD为4米,从G点测得广告牌顶端F点和底端E点的仰角分别是60°和45°.
(1)若AF长为5米,求灯牌的面积;
(2)求两侧加固的铝合金框架总共用料多少米?(本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+3(1-k)(其中k为常数,k≠0),k取不同数值时,可得不同直线,请探究这些直线的共同特征.
实践操作
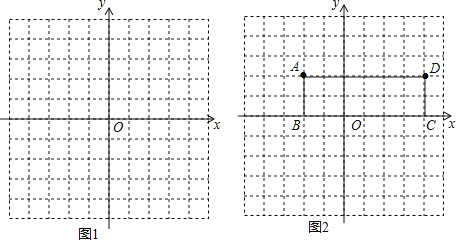
(1)当k=1时,直线l1的解析式为 ,请在图1中画出图象;当k=2时,直线l2的解析式为 ,请在图2中画出图象;
探索发现
(2)直线y=kx+3(1-k)必经过点( , );
类比迁移
(3)矩形ABCD如图2所示,若直线y=kx+k-2(k≠0)分矩形ABCD的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com