
����Ŀ����ͼ����������A���ʾ����3��B���ʾ��b��C���ʾ��c����b.c����![]()
![]()
��1��b= ��c= ��
��2����ʹC.B����ľ�����A.B����ľ����2�������轫��C�����ƶ� ����λ���ȣ�
��3����A.B.C��ʼ���������˶�������A��ÿ��m����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�룻
�ٵ�A.B.C��ʾ�����ֱ��� . . ���ú�m.t�Ĵ���ʽ��ʾ����
������B���C֮��ľ����ʾΪd1����A���B֮��ľ����ʾΪd2����mΪ��ֵʱ��2d1��d2��ֵ��������ʱ��t�ı仯���ı䣬�������ʱ2d1��d2��ֵ��
���𰸡���1��b=-1��c=4��
(2) 1��9��
��3����-3-mt��-1+2t��4+5t����m=4��2d1��d2��ֵΪ12��
��������
��1����![]() ������ƽ��������ֵ�ķǸ��Կɵ�b+1=0��c-4=0���ݴ˿����b��c��ֵ��
������ƽ��������ֵ�ķǸ��Կɵ�b+1=0��c-4=0���ݴ˿����b��c��ֵ��
��
��2�������AB��BC�ij��ȣ�������ἴ�ɵó���C�����ƶ��ľ��룬�����⣻
��3���ٽ��·��=ʱ�����ٶ�д���𰸣�
�ڸ��ݢ��ȱ�ʾ��d1��d2���Ӷ���ʾ��2d1-d2��Ȼ�����2d1��d2��ֵ��������ʱ��t�ı仯���ı�ó�t��ϵ��Ϊ0���������m��ֵ���̶����2d1��d2��ֵ.
�⣺��1����![]()
��b+1=0��c-4=0
��b=-1��c=4
(2)�������֪��AB= 2��
��B C=4��
���C�����ƶ��������3��-5
���轫��C�����ƶ�1��9����λ��
�ʴ��ǣ�1��9��
��3���ٵ�A��ʾ������-3-mt����B��ʾ������-1+2t����C����ʾ������4+5t��
�ʴ��ǣ�-3-mt��-1+2t��4+5t��
�ڡߵ�A��ʾ������-3-mt����B��ʾ������-1+2t����C����ʾ������4+5��
��d1=4+5t-(-1+2t)=3t+5��d2=-1+2t-(-3-mt)=��m+2��t+2��
��2d1-d2=2��3t+5��-[��m+2��t+2]=��4-m��t+12��
��2d1��d2��ֵ��������ʱ��t�ı仯���ı�
��4-m=0��
��m=4��
�ʵ�m=4ʱ��2d1��d2��ֵ��������ʱ��t�ı仯���ı䣬��ʱ2d1��d2��ֵΪ12��


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����![]() ��
��![]() ����Ʒ�Ƶ�ϴ�»������ۼ��ۼ����±���
����Ʒ�Ƶ�ϴ�»������ۼ��ۼ����±���
Ʒ�� |
|
|
���ۣ�Ԫ/̨�� | 1500 | 1800 |
�ۼۣ�Ԫ/̨�� | 1800 | 2200 |
��1�����̳�9�·���45000Ԫ����![]() ��
��![]() ����Ʒ�Ƶ�ϴ�»���ȫ����������9600Ԫ�����̳�9�·ݹ���
����Ʒ�Ƶ�ϴ�»���ȫ����������9600Ԫ�����̳�9�·ݹ���![]() ��
��![]() ����ϴ�»���������
����ϴ�»���������
��2�����̳�10�·��ֹ���![]() ��
��![]() ����Ʒ�Ƶ�ϴ�»�����ȥ36000Ԫ
����Ʒ�Ƶ�ϴ�»�����ȥ36000Ԫ
���ʸ��̳����м��ֽ�����������������з����г�����
��ͨ������˵��ϴ�»�ȫ������������ֽ�����������õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=x2+mx+1����0��x��2ʱ�ĺ���ֵ���ǷǸ�������ʵ��m��ȡֵ��ΧΪ��������
A. m�ݩ�2 B. ��4��m�ܩ�2 C. m�ݩ�4 D. m�ܩ�4��m�ݩ�2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�˫ʮ�����ڼ䣬A��B�������п�չ����������ʽ���£�
A���У��������9�ۺ�������2000Ԫ���Ż�300Ԫ��
B�����������8����
ijѧУ�ƻ�����ijƷ�Ƶ���������Ʒ����Ʒ�Ƶ�������A��B�������еı����ͬ�������̳��Ļ��ʽ��
��1����һ���Ը���4200Ԫ����������������B�̳��������������A�̳������������5�����������������ı����
��2��ѧУ�ƻ�����100�������������һ��������ʹ����ķ�����������ֱ��д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ڱ�ֱ�ĺ��߹�·��ͬ��㡢ͬ�յ㡢ͬ�������ٲ���2400�ף��ȵ��յ����ԭ����Ϣ����֪���ȳ���4���ӣ����������й����У��ס������˵ľ���y���ף���׳�����ʱ��t���֣�֮��Ĺ�ϵ��ͼ��ʾ�����н��ۣ�
���ײ��е��ٶ�Ϊ60��/�֣�
��������ȫ������32���ӣ�
������16�����ϼף�
���ҵ����յ�ʱ�������յ㻹��300��
������ȷ�Ľ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߣ�y=ax2+bx+c��a��0������A��2��4����B����1��1�����㣬��������Ϊ��h��k������������ȷ���۵�����ǣ�������
��b��1����c��2����h��![]() ����k��1��
����k��1��
A. �٢ڢۢ� B. �٢ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����M��x���ϣ��Ե�MΪԲ�ģ�2.5��Ϊ�뾶��Բ��y����A��B���㣬��x����C��x1��0����D��x2��0�����㣬��x1��x2����x1��x2�Ƿ���x��2x+1��=��x+2��2��������
��1�����C��D����M�����ꣻ
��2����ֱ��y=kx+b�С�M�ڵ�A����x����P����PA�ij���
��3����M���Ƿ���������ĵ�Q��ʹ��Q��A��C���㹹�ɵ�����������AOC���ƣ������ڣ������������꣬�������A��C��Q����������ߵĽ���ʽ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������C�ڰ�Բ�⣬AC��BC���Բ����D���E�㣮
��1����ֻ���̶ȵ�ֱ��������ABC���������ߣ���д��������
��2����AC=AB������DE��BE����֤��DE=BE��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1��CΪ�߶� AB��һ�㣬�� AC��BCΪһ�ߣ��� ABͬ���������� ACDE�ͳ����� CBFG���� ���� AC=2AE��CB=2BF���� AC2a��BC2b(a b) .
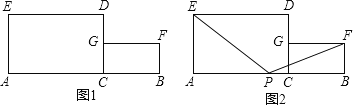
��1���dz����� ACDE�����Ϊ s1 �������� CBFG�����Ϊ s2 .�� AB6, a2b ���� s1 s2 .
��2����ͼ 2���� P���߶� CA�ϵĶ���.
�ٵ��� P�ӵ� C�����ƶ�![]() ����λ������EAP����FBP�����֮��.
����λ������EAP����FBP�����֮��.
�ڵ��� P�ӵ� C�����ƶ� ![]() ����λ����EAP����FBP�����֮���Ϊ m1 �� ���� P�ӵ� C�����ƶ� (a b) ����λ����EAP����FBP�����֮���Ϊ m2 ����
����λ����EAP����FBP�����֮���Ϊ m1 �� ���� P�ӵ� C�����ƶ� (a b) ����λ����EAP����FBP�����֮���Ϊ m2 ���� ![]() ��ֵ������ú� n �Ĵ���ʽ��ʾ��.
��ֵ������ú� n �Ĵ���ʽ��ʾ��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com