
分析 先把分母因式分解和除法化为乘法运算,再约分,然后进行同分母的减法运算,最后把x的值代入计算即可.
解答 解:原式=$\frac{{x}^{2}}{(x+2)^{2}}$•$\frac{x+2}{x}$-$\frac{x-1}{x+2}$
=$\frac{x}{x+2}$-$\frac{x-1}{x+2}$
=$\frac{x-x+1}{x+2}$
=$\frac{1}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{1}{\sqrt{2}-2+2}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


科目:初中数学 来源: 题型:选择题
| A. | (2,9) | B. | (5,3) | C. | (-4,2) | D. | (-9,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
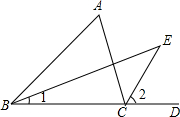 请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.
请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
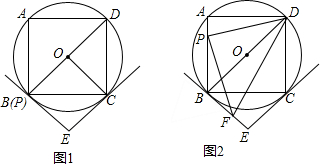
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<2 | B. | m<0 | C. | m>2 | D. | m>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com