
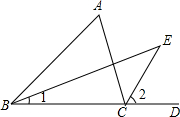
 请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.
请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.分析 根据三角形的外角的性质,结合图形证明即可.
解答 证明:因为BE是∠ABC的平分线,CE是∠ACD的平分线,
所以∠ABC=2∠1,∠ACD=2∠2.(角平分线的定义)
因为∠ACD是△ABC的一个外角,
所以∠ACD=∠A+∠ABC.(三角形的一个外角等于与它不相邻的两个内角的和)
所以∠A=∠ACD-∠ABC.(等式的性质)
所以∠A=2∠2-2∠1.(等量代换)
=2(∠2-∠1),
因为∠2是△BEC的一个外角,
所以∠2=∠1+∠E.(三角形的一个外角等于与它不相邻的两个内角的和)
所以∠E=∠2-∠1.(等式的性质)
所以∠A=2∠E.(等量代换)
故答案为:角平分线的定义;三角形的一个外角等于与它不相邻的两个内角的和;等式的性质;等量代换;三角形的一个外角等于与它不相邻的两个内角的和;等式的性质;等量代换.
点评 本题考查的是三角形的外角的性质以及几何证明,掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:解答题
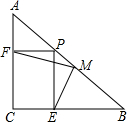 已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明:
已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
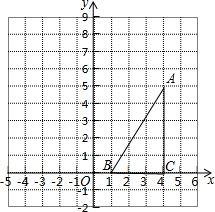 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度后,再沿y轴向上平移2个单位,根据所给的直角坐标系(O是坐标原点),解答下列问题:
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度后,再沿y轴向上平移2个单位,根据所给的直角坐标系(O是坐标原点),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,1) | B. | (-2,-1) | ||
| C. | (2,-1) | D. | (1,2),(-1,2),(1,-2),(-1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
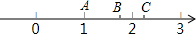 如图,数轴上A、B两点对应的实数分别为1和$\sqrt{3}$,若点A关于点B的对称点为C,则点C所对应的实数为2$\sqrt{3}$-1.
如图,数轴上A、B两点对应的实数分别为1和$\sqrt{3}$,若点A关于点B的对称点为C,则点C所对应的实数为2$\sqrt{3}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com