
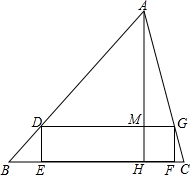
 如图,一块三角形土地的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面是矩形DEFG的大楼,设矩形DEFG的一边DE=x(m).当DE为多少时,大楼底面的面积最大?最大值是多少?
如图,一块三角形土地的底边BC=100m,高AH=80m.某单位要沿着底边BC修一座底面是矩形DEFG的大楼,设矩形DEFG的一边DE=x(m).当DE为多少时,大楼底面的面积最大?最大值是多少?科目:初中数学 来源: 题型:
 一艘海轮以30海里/时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/时的速度由南向北移动,距台风中心30
一艘海轮以30海里/时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/时的速度由南向北移动,距台风中心30| 10 |
| 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com