
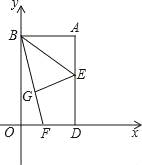
【题目】如图,以矩形ABOD的两边OD、OB为坐标轴建立直角坐标系,若E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交OD于F点.若OF=I,FD=2,则G点的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
连结EF,作GH⊥x轴于H,根据矩形的性质得AB=OD=OF+FD=3,再根据折叠的性质得BA=BG=3,EA=EG,∠BGE=∠A=90°,而AE=DE,则GE=DE,于是可根据“HL”证明Rt△DEF≌Rt△GEF,得到FD=FG=2,则BF=BG+GF=5.在Rt△OBF中,利用勾股定理计算出OB,然后根据△FGH∽△FBO,利用相似比计算出GH和FH,根据OH=OF﹣HF,即可得到G点的坐标.
连结EF,作GH⊥x轴于H,如图,
∵四边形ABOD为矩形,
∴AB=OD=OF+FD=1+2=3.
∵△ABE沿BE折叠后得到△GBE,
∴BA=BG=3,EA=EG,∠BGE=∠A=90°.
∵点E为AD的中点,
∴AE=DE,
∴GE=DE.
在Rt△DEF和Rt△GEF中,
∵![]() ,
,
∴Rt△DEF≌Rt△GEF(HL),
∴FD=FG=2,
∴BF=BG+GF=3+2=5.
在Rt△OBF中,OF=1,BF=5,
∴OB![]() .
.
∵GH∥OB,
∴△FGH∽△FBO,
∴![]() ,
,
即![]() ,
,
∴GH![]() ,FH
,FH![]() ,
,
∴OH=OF﹣HF=1![]() ,
,
∴G点坐标为(![]() ).
).
故选B.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
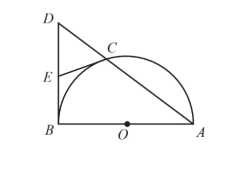
【题目】如图,AB 为半⊙O 的直径,弦 AC 的延长线与过点 B 的切线交于点 D,E 为 BD的中点,连接 CE.
(1)求证:CE 为 O 的切线;
(2)过点 C 作 CF AB ,垂足为点 F,AC=5,CF=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
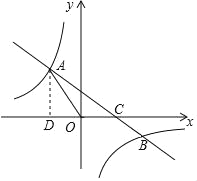
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)点E是x轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的课余生活,陶冶学生的情趣和爱好,某小学开展了学生社团活动。为了解学生参加活动的情况,学校进行了抽样调查,并做了如下的统计图,请根据统计图,完成以下问题
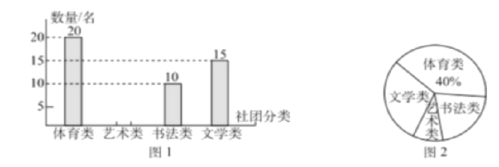
(1)本次调查共抽取了多少名学生?
(2)请补全条形统计图;
(3)若该中学共有![]() 名学生,请你估计该中学最想参加文学社团的学生约有多少名.
名学生,请你估计该中学最想参加文学社团的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
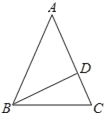
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com