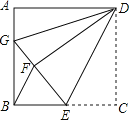
【题目】如图，正方形ABCD中，
，点E在边BC上，
，将
沿DE对折至
，延长EF交边AB于点C，连接DG，BF，给出以下结论：
≌
；
；
；
∽
，其中所有正确结论的个数是
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析：根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定Rt△ADG≌Rt△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，EG=10，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断④的正确性．
详解：由折叠可知，DF=DC=DA，∠DFE=∠C=90°， ∴∠DFG=∠A=90°，
在Rt△ADG和Rt△FDG中，AD=DF，DG=DG， ∴Rt△ADG≌Rt△FDG，故①正确；
∵正方形边长是12， ∴BE=EC=EF=6， 设AG=FG=x，则EG=x+6，BG=12-x，
由勾股定理得：
， 解得：x=4，
∴AG=GF=4，BG=8，EG=10， BG=2AG，故②、③正确；
BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，故④错误；则选C．
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案科目：初中数学 来源： 题型：
【题目】 如图，AB为⊙O的弦，C为劣弧AB的中点．
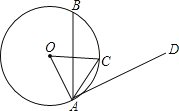
（1）若⊙O的半径为5，AB=8，求tan∠BAC；
（2）若∠DAC=∠BAC，且点D在⊙O的外部，判断AD与⊙O的位置关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
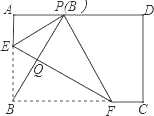
【题目】如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=
AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（ ）
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目：初中数学 来源： 题型：
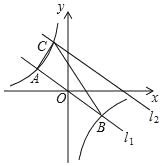
【题目】如图，在平面直角坐标系中，直线l1：y=﹣
x与反比例函数y=
的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2：
（1）求反比例函数的表达式；
（2）将直线l1：y=﹣x向上平移后的直线l2与反比例函数y=在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．
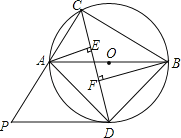
（1）求证：DP∥AB；
（2）若AC=6，BC=8，求线段PD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
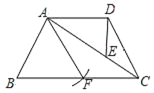
【题目】如图，已知梯形ABCD中，AD∥BC，AB=CD，点E在对角线AC上，且满足∠ADE=∠BAC．
（1）求证：CDAE=DEBC；
（2）以点A为圆心，AB长为半径画弧交边BC于点F，联结AF．求证：AF2=CECA．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，
，求
的度数． （提示：作
）．
（2）如图2，
，当点
在线段
上运动时，
，求
与
、
之间的数量关系，并说明理由．
（3）在（2）的条件下，如果点在射线
上运动，请你直接写出与、之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，AB＝8，BC＝5，以点A为圆心，以任意长为半径作弧，分别交AD、AB于点P、Q，再分别以P、Q为圆心，以大于
PQ的长为半径作弧，两弧在∠DAB内交于点M，连接AM并延长交CD于点E，则CE的长为（ ）
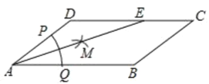
A. 3B. 5C. 2D. 6.5
查看答案和解析>>
科目：初中数学 来源： 题型：
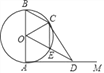
【题目】如图，AB是圆O的直径，射线AM⊥AB，点D在AM上，连接OD交圆O于点E，过点D作DC=DA交圆O于点C（A、C不重合），连接OC、BC、CE．
（1）求证：CD是⊙O的切线；
（2）若圆O的直径等于2，填空：
①当AD= 时，四边形OADC是正方形；
②当AD= 时，四边形OECB是菱形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com