
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
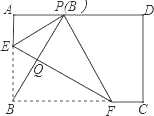
A. ①② B. ②③ C. ①③ D. ①④
【答案】D
【解析】试题解析:∵AE=![]() AB,
AB,
∴BE=2AE,
由翻折的性质得,PE=BE,
∴∠APE=30°,
∴∠AEP=90°﹣30°=60°,
∴∠BEF=![]() (180°﹣∠AEP)=
(180°﹣∠AEP)=![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠EFB=90°﹣60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,
∴EF=2PE,
∵EF>PF,
∴PF<2PE,故②错误;
由翻折可知EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,∠EFB=∠EFP=30°,
∴∠BFP=30°+30°=60°,
∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,
∴∠PBF=∠PFB=60°,
∴△PBF是等边三角形,故④正确;
综上所述,结论正确的是①④.
故选D.


科目:初中数学 来源: 题型:
【题目】为了培养学生的兴趣,我市某小学决定再开设A.舞蹈,B.音乐,C.绘画,D.书法四个兴趣班,为了解学生对这四个项目的兴趣爱好,随机抽取了部分学生进行调查,并将调查结果绘制成如图1,2所示的统计图,且结合图中信息解答下列问题:

(1)在这次调查中,共调查了多少名学生?
(2)请将两幅统计图补充完整;
(3)若本校一共有2000名学生,请估计喜欢“音乐”的人数;
(4)若调查到喜欢“书法”的4名学生中有2名男生,2名女生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到相同性别的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD(AB<AD).
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;
①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;
②作∠DAE的平分线交CD于点F;
③连接EF;
(2)在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解决问题.
对于形如![]() 这样的二次三项式,可以用公式法将它分解成
这样的二次三项式,可以用公式法将它分解成 ![]() 的形式.但对于二次三项式
的形式.但对于二次三项式![]() ,就不能直接运用公式了.此时,我们可以在二次三项式
,就不能直接运用公式了.此时,我们可以在二次三项式![]() 中先加上一项
中先加上一项 ![]() ,使它与
,使它与![]() 的和成为一个完全平方式,再减去
的和成为一个完全平方式,再减去![]() ,整个式子的值不变,于是有:
,整个式子的值不变,于是有:
![]()
像这样,先添﹣适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.
(1)利用“配方法”分解因式:![]() .
.
(2)若 a b 5 , ab 6 ,求:①![]() ;②
;② ![]() 的值.
的值.
(3)已知 x 是实数,试比较![]() 与
与![]() 的大小,说明理由.
的大小,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,![]() ,点E在边BC上,
,点E在边BC上,![]() ,将
,将![]() 沿DE对折至
沿DE对折至![]() ,延长EF交边AB于点C,连接DG,BF,给出以下结论:
,延长EF交边AB于点C,连接DG,BF,给出以下结论:![]() ≌
≌![]() ;
;![]() ;
;![]() ;
;![]() ∽
∽![]() ,其中所有正确结论的个数是
,其中所有正确结论的个数是![]()
![]()
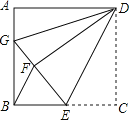
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
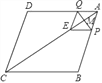
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com