
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.

【答案】(1)证明见解析;(2)等腰直角三角形.
【解析】试题分析:
(1)先证四边形ABDF是平行四边形,再证结论;
(2)由四边形ADCF是正方形来证明△ABC是等腰直角三角形.
试题解析:
(1)证明:∵点D、E分别是边BC、AC的中点,∴DE∥AB,
∵AF∥BC,∴四边形ABDF是平行四边形,∴AF=BD,则AF=DC=AD,
∵AF∥BC,∴四边形ADCF是平行四边形;
(2)当△ABC是等腰直角三角形时,四边形ADCF是正方形,
理由:∵四边形ADCF是正方形,∴∠ADC=90°,AC=DF,AF=DC.
∵点D,E分别是边BC,AC的中点,AB=2DE,∴AB=DF,所以AB=AC.
∴四边形ABDF是平行四边形,∴AF=BD,∴BD=CD=AD,
∴∠BAC=90°,
∴△ABC是等腰直角三角形.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:![]() 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到![]() 的图象,则
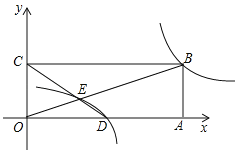
的图象,则![]() 是y与x的“反比例平移函数”.如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数
是y与x的“反比例平移函数”.如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数![]() ”的图象经过B、E两点.则这个“反比例平移函数”的表达式为____________;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,则写出这个反比例函数的表达式为________________ .
”的图象经过B、E两点.则这个“反比例平移函数”的表达式为____________;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,则写出这个反比例函数的表达式为________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:3+2=3×2-1,4+![]() =4×
=4×![]() -1,给出定义如下:
-1,给出定义如下:
我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(-2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AB为⊙O的弦,C为劣弧AB的中点.
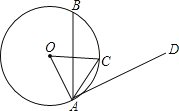
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知A、B两个边长不相等的正方形纸片并排放置,若m7,n3,试求A、B两个正方形纸片的面积之和.
(2)如图1,用m、n表示A、B两个正方形纸片的面积之和为 .(请直接写出答案)
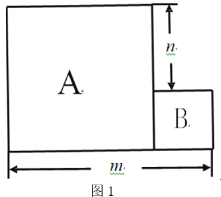
(3)如图2,若A、B两个正方形纸片的面积之和为5,且图2中阴影部分的面积为2,试求m、n的值.

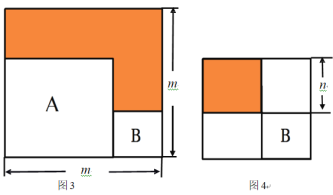
(4)现将正方形纸片A、B并排放置后构造新的正方形得图3,将正方形纸片B放在正方形纸片A的内部得图4,若图3和图4中阴影部分的面积分别为12和1,则A、B两个正方形纸片的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
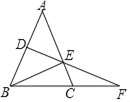
【题目】如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为2000m2的区域进行绿化,安排甲、乙两个工程队完成,已知甲队每天完成绿化的面积是乙队每天完成绿化的面积的2倍,并且在独立完成面积为600m2区域的绿化时,甲队比乙队少用6天.
(1)甲、乙两个工程队每天能完成绿化的面积分别是多少?
(2)若学校每天需付给甲队的绿化费用为0.5万元,乙队为0.3万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
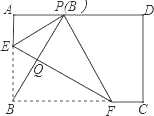
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() ,求
,求![]() 的度数. (提示:作
的度数. (提示:作![]() ).
).
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,求
,求![]() 与
与![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点![]() 在射线
在射线![]() 上运动,请你直接写出
上运动,请你直接写出![]() 与
与![]() 、
、![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com