
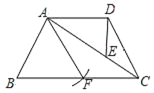
【题目】如图,已知梯形ABCD中,AD∥BC,AB=CD,点E在对角线AC上,且满足∠ADE=∠BAC.
(1)求证:CDAE=DEBC;
(2)以点A为圆心,AB长为半径画弧交边BC于点F,联结AF.求证:AF2=CECA.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据相似三角形的判定得出△ADE∽△CAB,再利用相似三角形的性质证明即可;
(2)根据相似三角形的判定得出△CDE∽△CAD,再利用相似三角形的性质证明即可.
试题解析:
证明(1)∵AD∥BC,
∴∠DAE=∠ACB,
∵∠ADE=∠BAC,
∴△ADE∽△CAB,
∴![]() ,
,
∴ABAE=DEBC,
∵AB=CD,
∴CDAE=DEBC;
(2)∵AD∥BC,AB=CD,
∴∠ADC=∠DAB,
∵∠ADE=∠BAC,
又∵∠ADC=∠ADE+∠CDE,∠DAB=∠BAC+∠CAD,
∴∠CDE=∠CAD,
∴△CDE∽△CAD,
∴![]() ,
,
∴CD2=CECA,
由题意,得AB=AF,AB=CD,
∴AF=CD,
∴AF2=CECA.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】24.在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
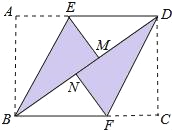
(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
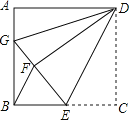
【题目】如图,正方形ABCD中,![]() ,点E在边BC上,
,点E在边BC上,![]() ,将
,将![]() 沿DE对折至
沿DE对折至![]() ,延长EF交边AB于点C,连接DG,BF,给出以下结论:
,延长EF交边AB于点C,连接DG,BF,给出以下结论:![]() ≌
≌![]() ;
;![]() ;
;![]() ;
;![]() ∽
∽![]() ,其中所有正确结论的个数是
,其中所有正确结论的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:x1,x2,x3,称为数列x1,x2,x3,计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为
,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,-1,3的价值为
,所以数列2,-1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列-1,2,3的价值为![]() ;数列3,-1,2的价值为1:…经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,-1,2的价值为1:…经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列4,3,-2的价值为______.
(2)将“4,3,-2”这三个数按照不同的顺序排列,可得到若干个数列,求这些数列的价值的最小值(请写出过程并作答).
(3)将3,-8,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为_______ (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下列等式:
第1个:22﹣1=1×3
第2个:32﹣1=2×4
第3个:42﹣1=3×5
第4个:52﹣1=4×6
第5个:62﹣1=5×7
…
这些等式反映出自然数间的某种运算规律.按要求解答下列问题:
(1)请你写出第6个等式: ;
(2)设n(n≥1)表示自然数,则第n个等式可表示为 ;
(3)运用上述结论,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励节约用电,某地用电标准规定:如果每户每月用电不超过![]() 度,那么每度按
度,那么每度按![]() 元缴纳;超过部分则按每度
元缴纳;超过部分则按每度![]() 元缴纳.
元缴纳.
(1)某户![]() 月份用电
月份用电![]() 度,共交电费
度,共交电费![]() 元,求
元,求![]() .
.
(2)若该户![]() 月份的电费平均每度
月份的电费平均每度![]() 元,求
元,求![]() 月份共用电多少度?应交电费多少元?
月份共用电多少度?应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
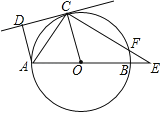
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上的一点,CE交⊙O于点F,连接OC,AC,若∠DAO=105°,∠E=30°.
(Ⅰ)求∠OCE的度数;
(Ⅱ)若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com