
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上的一点,CE交⊙O于点F,连接OC,AC,若∠DAO=105°,∠E=30°.
(Ⅰ)求∠OCE的度数;
(Ⅱ)若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
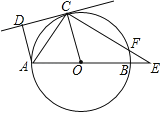
【答案】(Ⅰ)45°;(Ⅱ)2![]() ﹣2.
﹣2.
【解析】分析:
(1)由CD是⊙O的切线可得OC⊥CD,结合AD⊥CD于点D可得OC∥AD,从而可得∠COE=∠DAE=105°,结合∠E=30°即可得到∠OCE=45°;
(2)如下图,过点O作OM⊥CF于点M,则CM=MF结合∠OCE=45°,OC=![]() 即可得到OM=CM=2=MF,结合∠E=30°可得OE=2OM=4,则由勾股定理可得ME=
即可得到OM=CM=2=MF,结合∠E=30°可得OE=2OM=4,则由勾股定理可得ME=![]() ,从而可得EF=ME-MF=
,从而可得EF=ME-MF=![]() .
.
详解:
(Ⅰ)∵CD是⊙O的切线,
∴OC⊥CD,又AD⊥CD,
∴AD∥OC,
∴∠COE=∠DAO=105°,
又∵∠E=30°,
∴∠OCE=180°﹣∠COE﹣∠E=45°;
(Ⅱ)如下图,过点O作OM⊥CE于M,
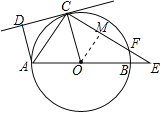
∴ CM=MF,∠OMC=∠OME=90°,
∵∠OCE=45°,
∴OM=CM=2=MF,
∵∠E=30°,
∴在Rt△OME中,OE=2OM=4,
∴ME=![]() ,
,
∴EF=ME-MF=![]() .
.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
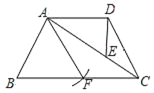
【题目】如图,已知梯形ABCD中,AD∥BC,AB=CD,点E在对角线AC上,且满足∠ADE=∠BAC.
(1)求证:CDAE=DEBC;
(2)以点A为圆心,AB长为半径画弧交边BC于点F,联结AF.求证:AF2=CECA.
查看答案和解析>>
科目:初中数学 来源: 题型:
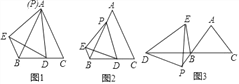
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从A地到B地,乙骑自行车从B地到A地两人都均速前进,已知两人在上午8点同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米.
(1)列方程,求A、B两地间的路程.
(2)请指出在解答时利用的等量关系是什么?
(3)请你利用其它的等量关系再列出方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
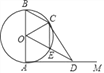
【题目】如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接OC、BC、CE.
(1)求证:CD是⊙O的切线;
(2)若圆O的直径等于2,填空:
①当AD= 时,四边形OADC是正方形;
②当AD= 时,四边形OECB是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足![]() =AD,连接CE并延长交AD于点F,连接AE,过点B作
=AD,连接CE并延长交AD于点F,连接AE,过点B作![]() 于点G,延长BG交AD于点H.在下列结论中:①
于点G,延长BG交AD于点H.在下列结论中:①![]() ;②
;②![]() ;③
;③![]() . 其中不正确的结论有( )
. 其中不正确的结论有( )
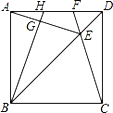
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
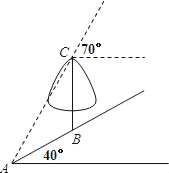
【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com