
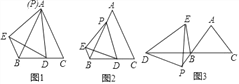
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)
【答案】(1)5;(2)4;(3)BD﹣BE =2acos55°.
【解析】试题分析:(1)先判断出∠BPE=∠CAD,进而判断出△PBE≌△ACD,即可得出BD+BE=BC=5;
(2)先构造出等边三角形,再判断出∠BPE=∠FPD,进而判断出△PBE≌△PFD,即可得出BD+BE=BF=4;
(3)类似于(2)的方法判断出△PBE≌△PFD得出BE=DF,再判断出BF=2BG,利用用锐角三角函数求出BG=acos55°,即可BD-BE=BF=2acos55°.
试题解析:解:(1)∵△ABC和△PDE是等边三角形,
∴PE=PD,AB=AC,∠DPE=∠CAB=60°,
∴∠BPE=∠CAD,
∴△PBE≌△ACD,
∴BE=CD,
∴BD+BE=BD+CD=BC=5,
故答案为5;
(2)如图2,过点P作PF∥AC交BC于F,
∴△FPB是等边三角形,
∴BF=PF=PB=AB﹣AP=4,∠BPF=60°,
∵△PDE是等边三角形,
∴PD=PE,∠DPE=60°,
∴∠BPE=∠FPD,
∴△PBE≌△PFD,
∴BE=DF,
∴BD+BE=BD+DF=BF=4;
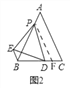
(3)如图3,
过点P作PF∥AC交BC于F,
∴∠BPF=∠BAC=70°,∠PFB=∠C,
∵AB=AC,∠BAC=70°,
∴∠ABC=∠C=55°,
∴∠PFB=∠C=∠PBF=55°,
∴PF=PB=a,
∵∠BPF=∠DPE=70°,
∴∠DPF=∠EPB,
∵PD=PE,
∴△PBE≌△PFD,
∴BE=DF,
过点P作PG⊥BC于G,
∴BF=2BG,
在Rt△BPG中,∠PBD=55°,
∴BG=BPcos∠PBD=acos55°,
∴BF=2BG=2acos55°,
∴BD﹣BE=BD﹣DF=BF=2acos55°.


科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下列等式:
第1个:22﹣1=1×3
第2个:32﹣1=2×4
第3个:42﹣1=3×5
第4个:52﹣1=4×6
第5个:62﹣1=5×7
…
这些等式反映出自然数间的某种运算规律.按要求解答下列问题:
(1)请你写出第6个等式: ;
(2)设n(n≥1)表示自然数,则第n个等式可表示为 ;
(3)运用上述结论,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励节约用电,某地用电标准规定:如果每户每月用电不超过![]() 度,那么每度按
度,那么每度按![]() 元缴纳;超过部分则按每度
元缴纳;超过部分则按每度![]() 元缴纳.
元缴纳.
(1)某户![]() 月份用电
月份用电![]() 度,共交电费
度,共交电费![]() 元,求
元,求![]() .
.
(2)若该户![]() 月份的电费平均每度
月份的电费平均每度![]() 元,求
元,求![]() 月份共用电多少度?应交电费多少元?
月份共用电多少度?应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
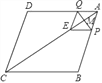
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
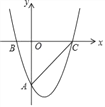
【题目】如图,抛物线y=![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“发展脐橙产业,加快脱贫的步伐”.某脐橙种植户新鮮采摘了20筐脐橙,以每筐25千克为标准重量,超过或不足干克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:干克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)与标准重量比较,20筐脐橙总计超过或不足多少千克?
(2)若脐橙毎干克售价6.5元,则出售这20筐脐橙可获得多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
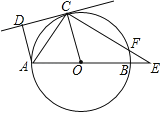
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上的一点,CE交⊙O于点F,连接OC,AC,若∠DAO=105°,∠E=30°.
(Ⅰ)求∠OCE的度数;
(Ⅱ)若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
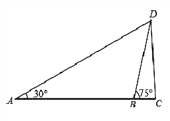
【题目】如图,为了测出某塔![]() 的高度,在塔前的平地上选择一点
的高度,在塔前的平地上选择一点![]() ,用测角仪测得塔顶
,用测角仪测得塔顶![]() 的仰角为
的仰角为![]() ,在
,在![]() 、
、![]() 之间选择一点
之间选择一点![]() (
(![]() 、
、![]() 、
、![]() 三点在同一直线上)用测角仪测得塔顶
三点在同一直线上)用测角仪测得塔顶![]() 的仰角为
的仰角为![]() ,且
,且![]() 间的距离为40m.
间的距离为40m.
(1)求点![]() 到
到![]() 的距离;
的距离;
(2)求塔高![]() (结果精确到0.1m.)(己知
(结果精确到0.1m.)(己知![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com