
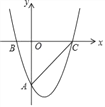
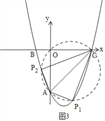
【题目】如图,抛物线y=![]() x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
x2+bx+c过点A(0,﹣6)、B(﹣2,0),与x轴的另一交点为点C.
(1)求此抛物线的解析式;
(2)将直线AC向下平移m个单位,使平移后的直线与抛物线有且只有一个公共点M,求m的值及点M的坐标;
(3)抛物线上是否存在点P,使△PAC为直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
【答案】(1)y=![]() x2﹣2x﹣6;(2)m=
x2﹣2x﹣6;(2)m=![]() ,M(3,﹣
,M(3,﹣![]() );(3)点P(2,﹣8),(﹣4,10),(1+
);(3)点P(2,﹣8),(﹣4,10),(1+![]() ,﹣5﹣
,﹣5﹣![]() ),(1﹣
),(1﹣![]() ,﹣5+
,﹣5+![]() ).
).
【解析】试题分析:(1)利用待定系数法求出二次函数的解析式;
(2)由直线向下平移m个单位得:y=x-6-m,由直线与抛物线有且只有一个公共点M可以知道:由解析式列方程组,根据△=0得出结论;
(3)分三种情况:
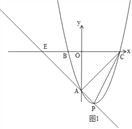
①当∠PAC=90°时,如图1,由△EAC是等腰直角三角形,可得E(-6,0),直线AP与抛物线的交点就是P,列方程组可得P点的坐标;
②当∠ACP=90°时,如图2,由PE=EC,列式:![]() x2-2x-6=-x-6,解出即可;
x2-2x-6=-x-6,解出即可;
③当∠APC=90°时,如图3,画图,根据直径所对的圆周角是直角,可知有两个点符合,设出P点的坐标,然后根据AC2,PA2,PC2的值,由勾股定理可得关于P点横、纵坐标的等量关系,联立抛物线的解析式,即可求出此时点P的坐标.
试题解析:解:(1)把点A(0,﹣6)、B(﹣2,0)代入抛物线y=![]() x2+bx+c中得:
x2+bx+c中得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣2x﹣6;
x2﹣2x﹣6;
(2)y=![]() x2﹣2x﹣6,
x2﹣2x﹣6,
当y=0时,![]() x2﹣2x﹣6=0,
x2﹣2x﹣6=0,
解得:x1=﹣2,x2=6,
∴C(6,0);
设直线AC的解析式为:y=kx+b,
则![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=x﹣6,
直线AC向下平移m个单位后的直线关系式为:y=x﹣6﹣m,
∵平移后的直线与抛物线有且只有一个公共点M,
则![]() ,
,
得:![]() =0,
=0,
△=(﹣3)2﹣4×![]() m=0,
m=0,
m=![]() ,
,
代入得:y=x﹣6﹣m=x﹣![]() ,
,
则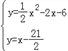 ,
,
解得:![]() ,
,
∴M(3,﹣![]() );
);
(3)分三种情况:
①当∠PAC=90°时,如图1,
∵OA=OC=6,∠AOC=90°,
∴△AOC是等腰直角三角形,
∴∠ACO=45°,
∴△EAC是等腰直角三角形,
∴AE=AC,
∴OE=OC=6,
∴E(﹣6,0),
设AE:y=kx+b,
则![]() ,解得:
,解得:![]() ,
,
∴直线AE的解析式为:y=﹣x﹣6,
则![]() ,
,
![]() ﹣2x﹣6=﹣x﹣6,
﹣2x﹣6=﹣x﹣6,
解得:x1=0(舍),x2=2,
∴P(2,﹣8),
②当∠ACP=90°时,如图2,
∠PCB=90°﹣45°=45°,
过P作PE⊥BC于E,
∴△PEC是等腰直角三角形,
∴PE=EC,
设P(x,![]() x2﹣2x﹣6),
x2﹣2x﹣6),
∴PE=![]() x2﹣2x﹣6,EC=﹣x﹣6,
x2﹣2x﹣6,EC=﹣x﹣6,
∴![]() x2﹣2x﹣6=﹣x﹣6,
x2﹣2x﹣6=﹣x﹣6,
解得:x1=6,x2=﹣4,
∵P在第二象限,
∴x=6不符合题意,舍去,x=﹣4,
∴P(﹣4,10),
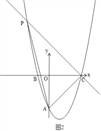
③以AC为直径画圆,交抛物线于两点P1、P2,如图3,
则∠AP1C=∠AP2C=90°,
∵![]() =
=![]() ,
,
![]() =
=![]() ,
,
AC2=62+62=72,
由勾股定理得:![]() +
+![]() =72,
=72,
化简得:x3﹣8x2+8x+24=0,
x3﹣2x2﹣4x﹣(6x2﹣12x﹣24)=0,
x(x2﹣2x﹣4)﹣6(x2﹣2x﹣4)=0,
(x﹣6)(x2﹣2x﹣4)=0,
解得:x1=6(舍),x2=1+![]() ,x3=1﹣
,x3=1﹣![]() ,
,
∴P(1+![]() ,﹣5﹣
,﹣5﹣![]() )或(1﹣
)或(1﹣![]() ,﹣5+
,﹣5+![]() ),
),
综上所述,△PAC为直角三角形时,点P的坐标为:(2,﹣8),(﹣4,10),(1+![]() ,﹣5﹣
,﹣5﹣![]() ),(1﹣
),(1﹣![]() ,﹣5+
,﹣5+![]() ).
).


科目:初中数学 来源: 题型:
【题目】综合与实践
元且期间,我市各大商场掀起购物狂湖,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场 | 优惠活动 |
甲 | 全场按标价的 |
乙 | 实行“满 (如:顾客购衣服 |
丙 | 实行“满 |
根据以上活动信息,解决以下问题:
(1)三个 商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
(2)黄 先生发现在甲、乙商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
(3)丙商场又推出 “先打折”,“再满![]() 减
减![]() 元”的活动,张先生买了一件标价为
元”的活动,张先生买了一件标价为![]() 元的上衣,张先生发现竟然比没打折前多付了
元的上衣,张先生发现竟然比没打折前多付了![]() 元钱,问丙商场先打了多少折后再参加活动?
元钱,问丙商场先打了多少折后再参加活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
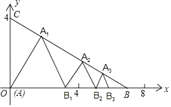
【题目】如图,已知,点A(0,0)、B(4![]() ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
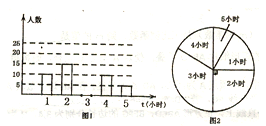
【题目】为了解某校八年级学生每周平均课外阅读时间的情况,随机抽查了该校八年级部分学生,对其每周平均课外阅读时间进行统计,根据统计数据绘制成如图的两幅尚不完整的统计图:
(1)本次共抽取了多少人?并请将图1的条形图补充完整;
(2)这组数据的众数是________;求出这组数据的平均数;
(3)若全校有1500人,请你估计每周平均课外阅读时间为3小时的学生多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
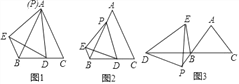
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一动点的初始位置位于数轴上的原点,现对该动点做如下移动:第1次从原点向右移动1个单位长度至![]() 点,第2次从
点,第2次从![]() 点向左移动3个单位长度至
点向左移动3个单位长度至![]() 点,第3次从
点,第3次从![]() 点向右移动6个单位长度至
点向右移动6个单位长度至![]() 点,第4次从
点,第4次从![]() 点向左移动9个单位长度至
点向左移动9个单位长度至![]() 点,…依此类推,移动2020次后该动点在数轴上表示的的数为______.
点,…依此类推,移动2020次后该动点在数轴上表示的的数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从A地到B地,乙骑自行车从B地到A地两人都均速前进,已知两人在上午8点同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米.
(1)列方程,求A、B两地间的路程.
(2)请指出在解答时利用的等量关系是什么?
(3)请你利用其它的等量关系再列出方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A. 当AB=BC时四边形ABCD是菱形
B. 当AC⊥BD时四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD且∠ABC=90°时四边形ABCD是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com