
 已知:如图,在△ABC中,AB=AC,点D是BC延长线上一点,点E是边AC上一点,如果∠EBC=∠D,BC=4,cos∠ABC=$\frac{1}{3}$.
已知:如图,在△ABC中,AB=AC,点D是BC延长线上一点,点E是边AC上一点,如果∠EBC=∠D,BC=4,cos∠ABC=$\frac{1}{3}$.分析 (1)由AB=AC,根据“等边对等角”得到一对角相等,由已知的两角相等,利用两对对应角相等的两三角形相似,得到三角形BCE与三角形DBA相似,由相似得比例得证;
(2)由$\frac{CE}{AB}$=$\frac{BC}{BD}$得CE=$\frac{4}{7}$AB=$\frac{4}{7}$AC,根据$\overrightarrow{CE}$=$\frac{4}{7}$$\overrightarrow{CA}$=$\frac{4}{7}$($\overrightarrow{BA}$-$\overrightarrow{BC}$)可得答案.
解答 解:(1)∵AB=AC,
∴∠ABC=∠ACB.
∵∠EBC=∠D,
∴△BCE∽△DBA.
∴$\frac{CE}{AB}$=$\frac{BC}{BD}$.
(2)∵$\frac{CE}{AB}$=$\frac{BC}{BD}$,BC=4,BD=7,
∴$\frac{CE}{AB}$=$\frac{4}{7}$,即CE=$\frac{4}{7}$AB,
又AB=AC,
∴CE=$\frac{4}{7}$AC,
∴$\overrightarrow{CE}$=$\frac{4}{7}$$\overrightarrow{CA}$=$\frac{4}{7}$($\overrightarrow{BA}$-$\overrightarrow{BC}$)=$\frac{4}{7}$(-$\overrightarrow{a}$-$\overrightarrow{b}$)=-$\frac{4}{7}$$\overrightarrow{a}$-$\frac{4}{7}$$\overrightarrow{b}$.
点评 本题主要考查相似三角形的判定与性质及向量的运算,熟练掌握相似三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:填空题
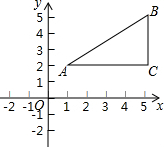 如图,在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E(点E不与点B重合),使△ACE和△ACB全等,写出所有满足条件的E点的坐标E1(5,-1),E2(1,-1),E3(1,5).
如图,在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E(点E不与点B重合),使△ACE和△ACB全等,写出所有满足条件的E点的坐标E1(5,-1),E2(1,-1),E3(1,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=ax2+bx+c的最大值为$\frac{13}{6}$,其图象经过点A(0,-2)、B(5,-2),点C在x轴上,∠ACB=90°,且CA<CB,将△ABC饶点A逆时针旋转,使点C的对应点C′落在x轴上.
如图,二次函数y=ax2+bx+c的最大值为$\frac{13}{6}$,其图象经过点A(0,-2)、B(5,-2),点C在x轴上,∠ACB=90°,且CA<CB,将△ABC饶点A逆时针旋转,使点C的对应点C′落在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:已知△ABC中,AB=AC,D为AB上一点,过D作DF⊥AB,交AC于E,交BC延长线于点F.求证:∠F=$\frac{1}{2}$∠A.
如图:已知△ABC中,AB=AC,D为AB上一点,过D作DF⊥AB,交AC于E,交BC延长线于点F.求证:∠F=$\frac{1}{2}$∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
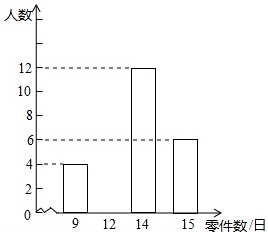 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
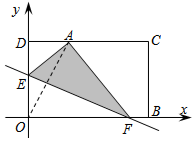 如图,在平面直角坐标系中,一张矩形纸片OBCD按图所示放置,已知OB=10,BC=6,将这张纸片折叠,使点O落在CD上,记作点A,折痕与边OD交于点E,与边OB交于点F,已知点E的坐标为(0,4),则点A的坐标为(2$\sqrt{3}$,6).
如图,在平面直角坐标系中,一张矩形纸片OBCD按图所示放置,已知OB=10,BC=6,将这张纸片折叠,使点O落在CD上,记作点A,折痕与边OD交于点E,与边OB交于点F,已知点E的坐标为(0,4),则点A的坐标为(2$\sqrt{3}$,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
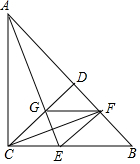 如图.在Rr△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线交CD于G,交BC于E,∠DCB的平分线交BD于F,连接EF,FG.
如图.在Rr△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线交CD于G,交BC于E,∠DCB的平分线交BD于F,连接EF,FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
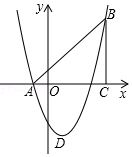 如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com