
 ��ͼ�����κ���y=ax2+bx+c�����ֵΪ$\frac{13}{6}$����ͼ����A��0��-2����B��5��-2������C��x���ϣ���ACB=90�㣬��CA��CB������ABC�ĵ�A��ʱ����ת��ʹ��C�Ķ�Ӧ��C������x���ϣ�
��ͼ�����κ���y=ax2+bx+c�����ֵΪ$\frac{13}{6}$����ͼ����A��0��-2����B��5��-2������C��x���ϣ���ACB=90�㣬��CA��CB������ABC�ĵ�A��ʱ����ת��ʹ��C�Ķ�Ӧ��C������x���ϣ����� ��1�����ö������������깫ʽ��$\frac{4ac-{b}^{2}}{4a}$�����һ���̣��ٰ�A��0��-2����B��5��-2���������������з��������⣻
��2���������ߣ�����ȫ�������Σ�֤����BCD�ա�B��C��E����B��E=BD=2��C��E=CD�����������Ƶã�AF�ij�Ϊ1��4����ΪAC��CB����AF=4���������⣬����ת�����ʵá�ACC���ǵ��������Σ������ߺ�һ�ã�OC=OC��=1���Ӷ����OE�ij����ó���B������꣬�����㵱x=3ʱ����Ӧ��yֵ������2�������������ϣ�������2�������������ϣ�
��3���ȸ��ݹ��ɶ�����B��P=$\frac{5}{2}$������S��B��PQ=S��OAP���������B��PQ��B��PΪ�ױ�ʱ�ĸ�Ϊ$\frac{6}{5}$������AB���ƽ�����Ҿ���Ϊ$\frac{6}{5}$���������߽���Q1��Q2������������ʽ�з�����ɵý��ۣ�
��� �⣺��1��������ã�$\left\{\begin{array}{l}{\frac{4ac-{b}^{2}}{4a}=\frac{13}{6}}\\{c=-2}\\{25a+5b+c=-2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{10}{3}}\\{c=-2}\end{array}\right.$��
����κ����Ľ���ʽΪ��y=-$\frac{2}{3}{x}^{2}+\frac{10}{3}x-2$��
��2����B��BD��x����D����B����B��E��x����E��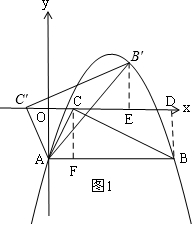
���C��EB��=��BDC=90�㣬
����ת�ã�BC=B��C�䣬AC=AC�䣬
���AC��C=��ACC�䣬
�ߡ�ACB=90�㣬
���BCD+��ACC��=90�㣬
�ߡ�AC��C+��B��C��C=90�㣬
���BCD=��B��C��C��
���BCD�ա�B��C��E��
��B��E=BD=2��C��E=CD��
��C��CF��AB��F��
��AF=x����BF=5-x��
�ߡ�CAB+��ACF=90�㣬��ACF+��FCB=90�㣬
���CAB=��FCB��
�ߡ�AFC=��BFC=90�㣬
���AFC�ס�CFB��
��$\frac{AF}{CF}=\frac{CF}{FB}$��
��CF2=AF•FB��
��B��5��-2����
��CF=2��
��22=x��5-x����
x2-5x+4=0��
��x-1����x-4��=0��
x=1��4��
��AC��CB��
��x=4���������⣬�ᣬ
��AF=OC=1��
��CD=BF=CE=5-1=4��
��AC=AC�䣬AO��CC�䣬
��OC=OC��=1��
��OE=C��E-OC��=4-1=3��
��B�䣨3��2����
��x=3ʱ��y=-$\frac{2}{3}$��9+$\frac{10}{3}$��3-2=2��
��B�����ڶ��κ�����ͼ���ϣ�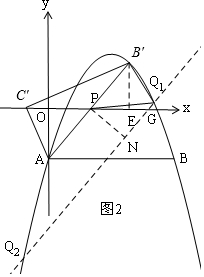
��3�����ڣ���AB��Ľ���ʽΪ��y=kx+b��
��A��0��-2����B�䣨3��2������ã�$\left\{\begin{array}{l}{b=-2}\\{3k+b=-2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-2}\end{array}\right.$��
��AB��Ľ���ʽΪ��y=$\frac{4}{3}$x-2��
��y=0ʱ��$\frac{4}{3}$x-2=0��
x=$\frac{3}{2}$��
��P��$\frac{3}{2}$��0����
��OP=$\frac{3}{2}$��
��������������һ��ΪQ1����Q1��AB���ƽ���ߣ�����������Q2����x����G����P��PN��AB����N����PN��Q1Q2��
��Rt��B��PE��B��E=2��PE=3-$\frac{3}{2}$=$\frac{3}{2}$��
�ɹ��ɶ����ã�B��P=$\sqrt{{2}^{2}+��\frac{3}{2}��^{2}}$=$\frac{5}{2}$��
��S��AOP=${S}_{��B��P{Q}_{1}}$��
��$\frac{1}{2}$��$\frac{3}{2}$��2=$\frac{1}{2}$��B��P•PN��
3=$\frac{5}{2}$PN��
PN=$\frac{6}{5}$��
�ߡ�B��PG+��GPN=90�㣬
��GPN+��PGN=90�㣬
���B��PG=��PGN��
�ߡ�PEB��=��PNG=90�㣬
���PNG�ס�B��EP��
��$\frac{PG}{PB��}=\frac{PN}{B��E}$��
��$\frac{PG}{\frac{5}{2}}$=$\frac{\frac{6}{5}}{2}$��
��PG=$\frac{3}{2}$��
��OG=OP+PG=$\frac{3}{2}$+$\frac{3}{2}$=3��
��G��3��0����
��GQ1�Ľ���ʽΪ��y=$\frac{4}{3}$x+b��
��G��3��0������ã�$\frac{4}{3}$��3+b=0��
b=-4��
��GQ1�Ľ���ʽΪ��y=$\frac{4}{3}$x-4��
��$\left\{\begin{array}{l}{y=\frac{4}{3}x-4}\\{y=-\frac{2}{3}{x}^{2}+\frac{10}{3}x-2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{x}_{1}=\frac{3+\sqrt{21}}{2}}\\{{y}_{1}=\frac{2\sqrt{21}-6}{3}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=\frac{3-\sqrt{21}}{2}}\\{{y}_{2}=\frac{-2\sqrt{21}-6}{3}}\end{array}\right.$��
������������Q�������ǣ�Q1��$\frac{3+\sqrt{21}}{2}$��$\frac{2\sqrt{21}-6}{3}$����Q2��$\frac{3-\sqrt{21}}{2}$��$\frac{-2\sqrt{21}-6}{3}$����
���� ���⿼���˴���ϵ��������κ�����һ�κ����Ľ���ʽ�������˷�����Ľ����������Ľ������ꣻ���������ƺ�ȫ�ȵ����ʺ��ж�֤���ߵij���д����Ӧ������꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD��CE�����۵���ʹ��B����AD���ϵĵ�F������AE=3��BE=5����AD���AB�ı�ֵ��5��4��
��ͼ��������ABCD��CE�����۵���ʹ��B����AD���ϵĵ�F������AE=3��BE=5����AD���AB�ı�ֵ��5��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ij���ŵ����ͼ�����������ͼ��ʾ���Ź���Բ���Σ����Ź��İ뾶Ϊ��������
��ͼ��ij���ŵ����ͼ�����������ͼ��ʾ���Ź���Բ���Σ����Ź��İ뾶Ϊ��������| A�� | 13m | B�� | 15m | C�� | 20 m | D�� | 26m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A����C��$\widehat{EB}$���е㣬�����н��ۣ���OC��AE����EC=BC���ۡ�DAE=��ABE����AC��OE��������ȷ���У�������
��ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A����C��$\widehat{EB}$���е㣬�����н��ۣ���OC��AE����EC=BC���ۡ�DAE=��ABE����AC��OE��������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��=30�� | B�� | ��=45�� | C�� | 30�㣼����45�� | D�� | 45�㣼����60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
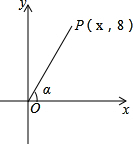 ��ͼ����ƽ��ֱ������ϵ�У���P�ڵ�һ�����ڣ��������ǣ�x��8������OP��x���������ļн�a������ֵ��$\frac{4}{3}$����
��ͼ����ƽ��ֱ������ϵ�У���P�ڵ�һ�����ڣ��������ǣ�x��8������OP��x���������ļн�a������ֵ��$\frac{4}{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���ڡ�ABC�У�AB=AC����D��BC�ӳ�����һ�㣬��E�DZ�AC��һ�㣬�����EBC=��D��BC=4��cos��ABC=$\frac{1}{3}$��
��֪����ͼ���ڡ�ABC�У�AB=AC����D��BC�ӳ�����һ�㣬��E�DZ�AC��һ�㣬�����EBC=��D��BC=4��cos��ABC=$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ABC�У���A=90�㣬��C=75�㣬AC=6��DE��ֱƽ��BC����BE��ֵΪ��������
��ͼ����ABC�У���A=90�㣬��C=75�㣬AC=6��DE��ֱƽ��BC����BE��ֵΪ��������| A�� | 12 | B�� | 6$\sqrt{3}$ | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com