
分析 (1)利用根的判别式建立关于m的方程求得方程的根即可;
(2)由根与系数的关系得出x1+x2=m-1,x1x2=2m-1,整理代入x12+x22=10,得出关于m的方程求得m,进一步利用根的判别式验证即可.
解答 解:(1)△=[-(m-1)]2-4(2m-1)=m2-10m+5,
∵△=-20,
∴m2-10m+5=-20
∴m2-10m+25=0
解得m1=m2=5
∴m=5;
(2)由根与系数的关系得x1+x2=m-1,x1x2=2m-1,
∴x12+x22=(x1+x2)2-2 x1x2=(m-1)2-2(2m-1)=10,
∴m2-6m-7=0,
解得:m1=7,m2=-1,
当m1=7时,△=m2-10m+5=-16<0 方程无实数根,不符合意愿,舍去;
当m2=-1时,△=m2-10m+5=16>0符合题意.
∴m=-1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了根与系数的关系.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
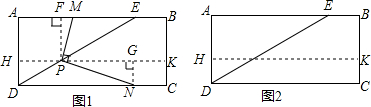
 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
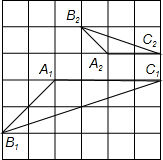 学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com