
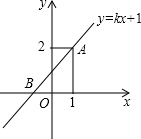
 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$). 分析 先把A(1,2)代入一次函数y=kx+1求出k的值,故可得出B点坐标,再分点P在x轴上与y轴上两种情况进行讨论.
解答  解:∵一次函数y=kx+1的图象过点A(1,2),
解:∵一次函数y=kx+1的图象过点A(1,2),
∴k+1=2,解得k=1,
∴一次函数的解析式为y=x+2,
∴B(-2,0).
当点P在x轴上时,P1(1,0);
当点P在y轴上时,设P(0,y),
∵∠APB=90°,
∴AP2+BP2=AB2,即12+(2-y)2+(-2)2+y2=(1+2)2+22,解得y=1±$\sqrt{2}$,
∴P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
故答案为:P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+3y=6 | B. | 2x-3y=3 | C. | 3x-2y=5 | D. | 3x+2y=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
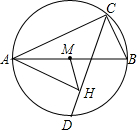 如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )
如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )| A. | 1 | B. | 1.5 | C. | 0.5 | D. | 0.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
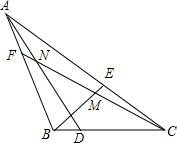 点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
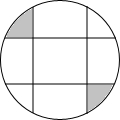 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )| A. | $\sqrt{2}$π | B. | 2-π | C. | π | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
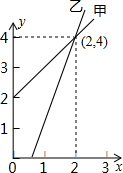 如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买甲家的1件售价约为3元,其中正确的说法是(填序号)①②③.
如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买甲家的1件售价约为3元,其中正确的说法是(填序号)①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com