
| A. | 2x+3y=6 | B. | 2x-3y=3 | C. | 3x-2y=5 | D. | 3x+2y=7 |
分析 根据k1•k2=-1,即可判定.
解答 解:∵3x+2y=6,
∴y=-$\frac{3}{2}$x+3,
k1=-$\frac{3}{2}$,
A、y=-$\frac{2}{3}$x+3,k2=-$\frac{2}{3}$,k1•k2≠-1故选项错误;
B、y=$\frac{2}{3}$x-1,k2=$\frac{2}{3}$,k1•k2=-1故选项正确;
C、y=$\frac{3}{2}$x-$\frac{5}{2}$,k2=$\frac{3}{2}$,k1•k2,≠-1故选项错误;
D、y=-$\frac{3}{2}$x+$\frac{7}{2}$,k2=-$\frac{3}{2}$,k1•k2≠-1故选项错误;
故选B.
点评 本题考查两条直线平行相交问题,记住结论直线y=k1x+b1与直线y=k2x+b2互相垂直,则有k1•k2=-1,两条直线平行k1=k2,b1≠b2,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
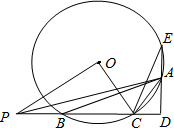 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E查看答案和解析>>
科目:初中数学 来源: 题型:填空题
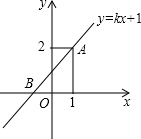 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?
浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com