
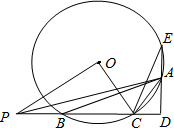
 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E分析 (1)由∠ACB+∠BEA=180°,∠ACB=120°,得∠BAE=60°,∠EBD=30°,根据∠EOC=2∠EBC即可解决问题.
(2)作OM⊥BC于M,利用△COM∽△CPO,得$\frac{CO}{CP}=\frac{CM}{CO}$,求出PC即可解决问题.
解答 (1)证明:如图 连接OE、BE、EC,
连接OE、BE、EC,
∵∠ACB+∠BEA=180°,∠ACB=120°,
∴∠BAE=60°,
∵ED⊥BD,
∴∠EDB=90°,∠EBD=90°-∠BAE=30°,
∴∠EOC=2∠EBC=60°,
∵OE=OC,
∴△OEC是等边三角形,
∴EC=OC=⊙O的半径.
(2)解:作OM⊥BC于M,
∵BC=6,OC=5,
∴MB=MC=3,OM=4,
∵∠OMC=∠COP=90°,∠MCO=∠PCO,
∴△COM∽△CPO,
∴$\frac{CO}{CP}=\frac{CM}{CO}$,
∴$\frac{5}{CP}=\frac{3}{5}$,
∴CP=$\frac{25}{3}$,
∴PB=CP-BC=$\frac{7}{3}$.
点评 本题考查三角形的外接圆的有关知识、圆内接四边形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是利用圆心角等于同弧所对的圆周角的2倍得到∠EOC=2∠EBC=60°,属于中考常考题型.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{25(x+y)=400-100}\\{50(y-x)=400+100}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{25(x+y)=400}\\{50(y-x)=100}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{25(x+y)=400-100}\\{50(y-x)=400}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{25(x+y)=400-100}\\{50(y-x)=100}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+3y=6 | B. | 2x-3y=3 | C. | 3x-2y=5 | D. | 3x+2y=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
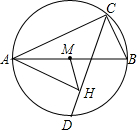 如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )
如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )| A. | 1 | B. | 1.5 | C. | 0.5 | D. | 0.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
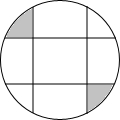 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )| A. | $\sqrt{2}$π | B. | 2-π | C. | π | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
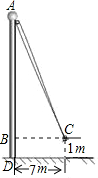 如图1,小红将升旗的绳子拉到旗杆顶端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆7m处,发现此时绳子末端距离地面1m,则绳子的长度为( )
如图1,小红将升旗的绳子拉到旗杆顶端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆7m处,发现此时绳子末端距离地面1m,则绳子的长度为( )| A. | 25m | B. | 4m | C. | 16m | D. | 17m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com