
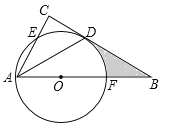
【题目】如图,如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若BD=![]() ,BF=2,求阴影部分的面积 (直接填空).
,BF=2,求阴影部分的面积 (直接填空).
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,利用角平分线和平行线之间的角度关系,得到OD//AC,所以OD⊥BC,从而得出BC与⊙O相切;
(2)利用直角三角形的勾股定理解得圆的半径,将阴影部分的面积转化为三角形面积与扇形面积之差,从而计算出阴影部分的面积.
(1)证明:如图,连接OD,
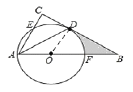
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠ODB=∠C=90°,
∵OD是⊙O的半径,
∴BC是⊙O的切线;
(2)设⊙O的半径为r,则OD=r,OB=r+2,
由(1)可知∠BDO=90°,
在Rt△BDO中,根据勾股定理可得:OD2+BD2=OB2,
即r2+(![]() )2=(r+2)2,
)2=(r+2)2,
解得:r=2,
在Rt△BOD中,tan∠BOD=![]() ,
,
∴∠BOD=60°,
故阴影部分的面积为:
S阴影=S△OBD-S扇形DOF=![]() ×OD×BD-
×OD×BD-![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】将等腰三角形![]() 折叠,使顶点
折叠,使顶点![]() 与底边
与底边![]() 的中点
的中点![]() 重合,折线分别交
重合,折线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
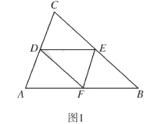
(2)如图2,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,并延长
,并延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以
,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以![]() 为一边的平行四边形)
为一边的平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
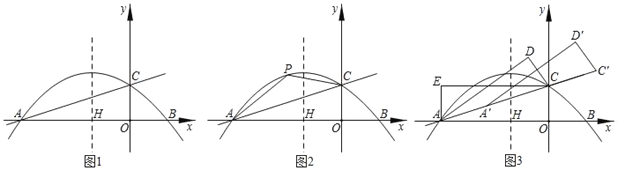
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品![]() 千克.
千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用![]() (元)与
(元)与![]() (千克)之间的函数关系式;
(千克)之间的函数关系式;
(2)若小明快递的物品超过1千克,则他应选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“南昌之星”摩天轮,位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园,摩天轮高![]() (最高点到地面的距离).如图,点
(最高点到地面的距离).如图,点![]() 是摩天轮的圆心,
是摩天轮的圆心,![]() 是其垂直于地面的直径,小贤在地面点
是其垂直于地面的直径,小贤在地面点![]() 处利用测角仪测得摩天轮的最高点
处利用测角仪测得摩天轮的最高点![]() 的仰角为
的仰角为![]() ,测得圆心
,测得圆心![]() 的仰角为
的仰角为![]() ,则摩天轮的半径为________
,则摩天轮的半径为________![]() (结果保留
(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() =
=![]() (
(![]() 为任意实数)
为任意实数)
(1)无论![]() 取何值,抛物线
取何值,抛物线![]() 恒过两点________,________.
恒过两点________,________.
(2)当![]() 时,设抛物线
时,设抛物线![]() 在第一象限依次经过整数点(横、纵坐标均为整数的点)为
在第一象限依次经过整数点(横、纵坐标均为整数的点)为![]() ,
,![]() …
…![]() .将抛物线
.将抛物线![]() 沿直线
沿直线![]()
![]() 平移,平移后的抛物线记为
平移,平移后的抛物线记为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() 的顶点为
的顶点为![]() (
(![]() ,例如
,例如![]() 时,抛物线
时,抛物线![]() 经过点
经过点![]() ,
,![]() 顶点为
顶点为![]() )
)
①抛物线![]() 的解析式为________;顶点坐标为________;
的解析式为________;顶点坐标为________;
②在抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,并判断四边形
的坐标,并判断四边形![]() 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
③直接写出线段![]() 的长________.
的长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年4月,过敏体质检测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:
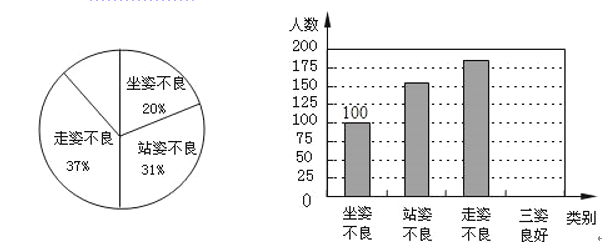
(1)请将两幅图补充完整;
(2)如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人.
(3)根据统计结果,请你简单谈谈自己的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com