
【题目】已知抛物线![]() :
:![]() =
=![]() (
(![]() 为任意实数)
为任意实数)
(1)无论![]() 取何值,抛物线
取何值,抛物线![]() 恒过两点________,________.
恒过两点________,________.
(2)当![]() 时,设抛物线
时,设抛物线![]() 在第一象限依次经过整数点(横、纵坐标均为整数的点)为
在第一象限依次经过整数点(横、纵坐标均为整数的点)为![]() ,
,![]() …
…![]() .将抛物线
.将抛物线![]() 沿直线
沿直线![]()
![]() 平移,平移后的抛物线记为
平移,平移后的抛物线记为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() 的顶点为
的顶点为![]() (
(![]() ,例如
,例如![]() 时,抛物线
时,抛物线![]() 经过点
经过点![]() ,
,![]() 顶点为
顶点为![]() )
)
①抛物线![]() 的解析式为________;顶点坐标为________;
的解析式为________;顶点坐标为________;
②在抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,并判断四边形
的坐标,并判断四边形![]() 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
③直接写出线段![]() 的长________.
的长________.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,
,![]() ;②存在,点
;②存在,点![]() 坐标为
坐标为![]() ;是矩形;③
;是矩形;③![]()
【解析】
(1)由抛物线C的解析式,令![]() 的系数为0,得出
的系数为0,得出![]() 的值,进而求出抛物线
的值,进而求出抛物线![]() 恒过的点的坐标;
恒过的点的坐标;
(2)①当![]() 时,抛物线C可化简为
时,抛物线C可化简为![]() ,根据题意,格点
,根据题意,格点![]() (2,4),根据抛物线平移的性质,可设平移后的抛物线为
(2,4),根据抛物线平移的性质,可设平移后的抛物线为![]() (m>0),将
(m>0),将![]() (2,4)代入,即可得解;
(2,4)代入,即可得解;
②用待定系数法求出抛物线![]() 和直线
和直线![]() 解析式,假设存在点
解析式,假设存在点![]() ,使得
,使得![]() ,求出直线
,求出直线![]() ,联立直线
,联立直线![]() 和抛物线
和抛物线![]() ,即可求出P点坐标;根据两点间距离公式求出
,即可求出P点坐标;根据两点间距离公式求出![]() 和
和![]() ,再结合勾股定理逆定理求出∠
,再结合勾股定理逆定理求出∠![]() =90°,即可判定四边形
=90°,即可判定四边形![]() 为矩形;
为矩形;
③由题意可设![]() ,将其代入平移后的抛物线
,将其代入平移后的抛物线![]() (m>0),求出m=2n-1,于是
(m>0),求出m=2n-1,于是![]() ,同理得出
,同理得出![]() ,由两点间距离公式即可得解.
,由两点间距离公式即可得解.
(1)![]() =
=![]()
令![]() ,
,
解得![]() 或
或![]()
将![]() 代入抛物线C的解析式,得
代入抛物线C的解析式,得![]() ,
,
将![]() 代入抛物线C的解析式,得
代入抛物线C的解析式,得![]() ,
,
∴无论![]() 取何值,抛物线
取何值,抛物线![]() 恒过两点
恒过两点![]() ,
,![]() ,
,
故答案为![]() ,
,![]() ;
;
(2)①当![]() 时,抛物线C:
时,抛物线C:![]() ,
,
根据题意,A1(1,1),A2(2,4),
设平移后的抛物线为![]() (m>0),
(m>0),
代入A2(2,4),得抛物线C2:![]()
解得,m=0(舍)或m=3
∴抛物线![]() 的解析式为
的解析式为![]() ,顶点坐标为(3,3).
,顶点坐标为(3,3).
故答案为:![]() ,
,![]() ;
;
②将A1(1,1)代入![]() (m>0),
(m>0),
得![]()
解得,m=0(舍)或m=1
∴抛物线![]() :
:![]() ,顶点坐标
,顶点坐标![]()
设直线![]() 的解析式为:
的解析式为:![]()
分别将A2(2,4)和M2(3,3)代入得
![]() ,解得
,解得![]()
∴直线![]() :
:![]()
假设存在点![]() ,使得
,使得![]() ,
,
设直线![]() 为
为![]() ,
,
将![]() 代入得
代入得![]() ,解得:t=2,
,解得:t=2,
所以直线![]() :
:![]()
联立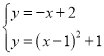 ,
,
解得![]() 或
或![]() (此点为M1)
(此点为M1)
∴存在点![]() ,使得
,使得![]() ,点
,点![]() 坐标为
坐标为![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
∴∠![]() =90°,
=90°,
∴四边形![]() 是矩形;
是矩形;
③设![]() ,将其代入平移后的抛物线
,将其代入平移后的抛物线![]() (m>0),
(m>0),
解得m=2n-1,于是![]() ,
,
同理可得:![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,ΔMCN面积为2cm?
(2)是否存在某一时刻t,使四边形APNC的面积为![]() cm?若存在,求t的值,若不存在,请说明理由;
cm?若存在,求t的值,若不存在,请说明理由;
(3)当t为何值时,以A、P、M为顶点的三角形与△ABC相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
x | -7 | -6 | -5 | -4 | -3 | -2 |
y | -27 | -13 | -3 | 3 | 5 | 3 |
①当x<-4时,y<3②当x=1时,y的值为-13;③-2是方程ax2+(b-2)x+c-7=0的一个根;④方程ax2+bx+c=6有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
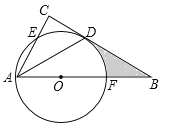
【题目】如图,如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若BD=![]() ,BF=2,求阴影部分的面积 (直接填空).
,BF=2,求阴影部分的面积 (直接填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的高速发展,人们的支付方式发生了巨大改变,某学习小组抽样调查了春节期间某商场顾客的支付方式,主要有现金支付、银联卡支付和手机支付,调查得知使用这三种支付的人数比为![]() ,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:
,手机支付已成为市民购物便捷支付方式.手机支付主要有以下三种方式:![]() ~支付宝,
~支付宝,![]() ~微信,
~微信,![]() ~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.
~其他.现将使用手机支付方式人数的调查结果绘制成如下不完整的统计图.

(1)扇形统计图中,![]() ________;请补全条形统计图;
________;请补全条形统计图;
(2)若该商场春节期间共20000人购物,请估计用支付宝进行支付的人数.
(3)经调查某天顾客现金支付、银联卡支付、手机支付每笔交易发生的平均金额分别为120元、260元、80元,求这天顾客每笔交易的平均金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今社会人们越来越离不开网络,电脑、手机被普遍使用,与此同时人们的视力也大大受到影响,2019年初某企业以25万元购得某项护目镜生产技术后,再投人100万元购买生产设备,进行该护目镜的生产加工,已知生产这种护目镜的成本价为每件20元,经过市场调研发现该产品的销售单价定在![]() 元比较合理,并且该产品的年销售量
元比较合理,并且该产品的年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式为
(元)之间的函数关系式为![]() .(年获利=年销售收入-生产成本-投资成本)
.(年获利=年销售收入-生产成本-投资成本)
(1)求该公司第一年的年获利![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(2)2020年初我国爆发新冠肺炎,该公司决定向红十字会捐款20万元,另外每销售一件产品,就抽出1元钱作为捐款,若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后,到2020年底,两年的总盈利不低于57.5万元,请你确定此时销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
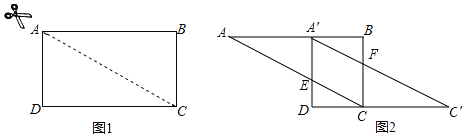
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 剪开,再把
剪开,再把![]() 沿
沿![]() 方向平移,得到图2,其中
方向平移,得到图2,其中![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)在图2中,除![]() 与
与![]() 外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;
外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;
(2)设![]() .①当
.①当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形?②设四边形
是菱形?②设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,
时,![]() 点坐标为
点坐标为![]() ;当
;当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,则称点
,则称点![]() 为点
为点![]() 的
的![]() 分变换点(其中
分变换点(其中![]() 为常数).例如:
为常数).例如:![]() 的0分变换点坐标为
的0分变换点坐标为![]() .
.
(1)点![]() 的1分变换点坐标为 ;点
的1分变换点坐标为 ;点![]() 的1分变换点在反比例函数
的1分变换点在反比例函数![]() 图像上,则
图像上,则![]() ;若点
;若点![]() 的1分变换点直线
的1分变换点直线![]() 上,则
上,则![]() ;
;
(2)若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的3分变换点.
的3分变换点.
①直写出点![]() 所在函数的解析式;
所在函数的解析式;
②求点![]() 所在函数的图像与直线
所在函数的图像与直线![]() 交点坐标;
交点坐标;
③当![]() 时,点
时,点![]() 所在函数的函数值
所在函数的函数值![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
(3)点![]() ,
,![]() ,若点
,若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的
的![]() 分变换点.当点
分变换点.当点![]() 所在函数的图像与线段
所在函数的图像与线段![]() 有两个公共点时,直接写出
有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com