
【题目】如图,已知![]() 、
、![]() 分别为
分别为![]() 的直径和弦,
的直径和弦,![]() 为
为![]() 的中点,
的中点,![]() 垂直于
垂直于![]() 的延长线于
的延长线于![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,下列结论一定错误的是( )
,下列结论一定错误的是( )
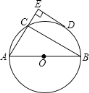
A. DE是⊙O的切线 B. 直径AB长为20cm
C. 弦AC长为16cm D. C为![]() 的中点
的中点
【答案】D
【解析】
AB是圆的直径,则∠ACB=90°,根据DE垂直于AC的延长线于E,可以证得ED∥BC,则DE⊥OD,即可证得DE是圆的切线,根据切割线定理即可求得AC的长,连接OD,交BC与点F,则四边形DECF是矩形,根据垂径定理即可求得半径.
解答:解:连接OD,OC.
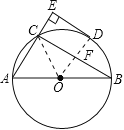
∵D是弧BC的中点,则OD⊥BC,
∴DE是圆的切线.故A正确;
∴DE2=CE?AE
即:36=2AE
∴AE=18,则AC=AE-CE=18-2=16cm.故C正确;
∵AB是圆的直径.
∴∠ACB=90°,
∵DE垂直于AC的延长线于E.
D是弧BC的中点,则OD⊥BC,
∴四边形CFDE是矩形.
∴CF=DE=6cm.BC=2CF=12cm.
在直角△ABC中,根据勾股定理可得:AB=![]() =
=![]() =20cm.故B正确;
=20cm.故B正确;
在直角△ABC中,AC=16,AB=20,
则∠ABC≠30°,
而D是弧BC的中点.
∴弧AC≠弧CD.
故D错误.
故选D.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,﹣3),并且以x=1为对称轴.
(1)求此函数的解析式;
(2)作出二次函数的大致图象;
(3)在对称轴x=1上是否存在一点P,使△PAB中PA=PB?若存在,求出P点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 相离,
相离,![]() 于点
于点![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .若
.若![]() 上存在点
上存在点![]() ,使
,使![]() 是以
是以![]() 为底边的等腰三角形,则半径
为底边的等腰三角形,则半径![]() 的取值范围是:________.
的取值范围是:________.
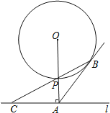
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 .
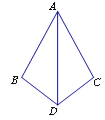
查看答案和解析>>
科目:初中数学 来源: 题型:
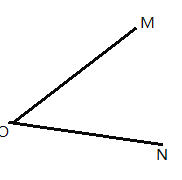
【题目】如图,已知![]() .
.
(1)用直尺和圆规画出![]() 的平分线
的平分线![]() (保留作图痕迹,不写作法,不用证明)
(保留作图痕迹,不写作法,不用证明)
(2)在射线![]() 上任意选取一点
上任意选取一点![]() ,再在射线
,再在射线![]() 上选取一点
上选取一点![]() ,要求
,要求![]() 为钝角.
为钝角.
①在射线![]() 上找到所有使得
上找到所有使得![]() 的点
的点![]() .
.
②写出![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
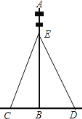
【题目】如图,为了使电线杆稳固的垂直于地面,两侧常用拉紧的钢丝绳索固定,由于钢丝绳的交点![]() 在电线杆的上三分之一处,所以知道
在电线杆的上三分之一处,所以知道![]() 的高度就可以知道电线杆
的高度就可以知道电线杆![]() 的高度了.要想得到
的高度了.要想得到![]() 的高度,需要测量出一些数据,然后通过计算得出.
的高度,需要测量出一些数据,然后通过计算得出.
请你设计出要测量的对象:________;
请你写出计算![]() 高度的思路:________.
高度的思路:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
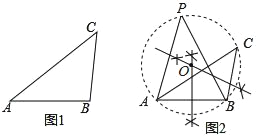
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com