
【题目】阅读下面的材料,并解答问题:
问题1:已知正数,有下列命题
![]()
![]()
![]()
根据以上三个命题所提供的规律猜想:![]() ,
,
以上规律可表示为a+b ![]()
问题2:建造一个容积为8立方米,深2米的长方形无盖水池,池底和池壁的造价分别为每平方米120元和80元。
(1)设池长为x米,水池总造价为y(元),求y和x的函数关系式;
(2)应用“问题1”题中的规律,求水池的最低造价
【答案】(1)![]() ;≥;(2)①y=480+320(
;≥;(2)①y=480+320( ![]() );②水池的最低造价为1760元
);②水池的最低造价为1760元
【解析】试题分析:问题1:根据以上三个命题所提供的规律猜想可得出结论.
问题2:(1)设池长为x米,水池总造价为y(元),由容积=底面积×高,得池宽为![]() ,y=480+320x+
,y=480+320x+![]() .
.
(2)周长最短,正方形周长最短,a+b=2![]() ,这样得出池壁面积为16米,进而算出总造价.
,这样得出池壁面积为16米,进而算出总造价.
试题解析:问题1:根据以上三个命题所提供的规律猜想可得:![]() ;≥.
;≥.
问题2:(1)设池长为x米,水池总造价为y(元),由容积=底面积×高,得池宽为![]() ,y=480+320x+
,y=480+320x+![]() .
.
(2)底面积:8÷2=4平米,
周长最短为:8米(正方形周长最短),a+b=2![]() ,
,
池壁面积:8×2=16平米,
总造价为:120×4+16×80=1760元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() 的图象相交于点B(m,1).
的图象相交于点B(m,1).
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
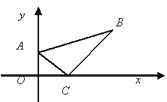
【题目】如图,已知以点A(0,1)、C(1,0)为顶点的△ABC中,∠BAC=60°,∠ACB=90°,在坐标系内有一动点P(不与A重合),以P、B、C为顶点的三角形和△ABC全等,则P点坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A﹣C路径向终点C运动;点Q从B点出发沿B﹣C﹣A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为_________时,△PEC与△QFC全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组五名同学在期末模拟考试(满分为120)的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值可以是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高台县为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;巷道镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)骆驼城镇改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=-1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是-1≤x<3 ;
⑤当x<0时,y随x增大而增大;
其中正确的个数是 ( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com