练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是某校体育场内一看台的截面图，看台CD与水平线的夹角为30°，最低处C与地面的距离BC为2.5米，在C，D正前方有垂直于地面的旗杆EF，在C，D两处测得旗杆顶端F的仰角分别为60°和30°，CD长为10米，升旗仪式中，当国歌开始播放时，国旗也在离地面1.5米的P处同时冉冉升起，国歌播放结束时，国旗刚好上升到旗杆顶端F，已知国歌播放时间为46秒，求国旗上升的平均速度．（结果精确到0.01米/秒）

    【答案】国旗上升的平均速度约为0.35米/秒．

    【解析】

    先证明△DCF是直角三角形，然后根据正切的概念求出FC的长，再根据正弦的概念求出FG的长，结合图形计算即可．

    解：由题意得，∠FCD＝90°，∠FDC＝60°，

    ∴FC＝CDtan∠FDC＝10，

    在Rt△CGF中，FG＝FCsin∠FCG＝10×＝15，

    ∴PF＝FG+GE﹣PE＝15+2.5﹣1.5＝16，

    16÷46≈0.35，

    答：国旗上升的平均速度约为0.35米/秒．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

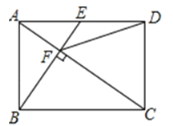
    【题目】在矩形ABCD中，点E为AD的中点，连接BE、AC，AC⊥BE于点F，连接DF，对于结论①CF=2AF②△AEF∽△CAB③DF=DC④tan∠CAD=正确的有_______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在某海域，一般指挥船在C处收到渔船在B处发出的求救信号，经确定，遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上，且BC=60海里；指挥船搜索发现，在C处的南偏西60°方向上有一艘海监船A，恰好位于B处的正西方向.于是命令海监船A前往搜救，已知海监船A的航行速度为30海里/小时，问渔船在B处需要等待多长时间才能得到海监船A的救援？（参考数据：，，结果精确到0.1小时）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

    （1）求甲、乙两种树苗每棵的价格各是多少元？

    （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

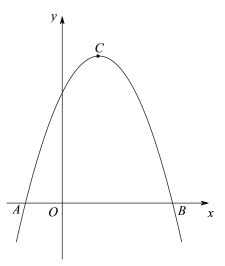
    【题目】如图，在平面直角坐标系xOy中，二次函数（a、b都是常数，且a<0）的图像与x轴交于点、，顶点为点C.

    （1）求这个二次函数的解析式及点C的坐标；

    （2）过点B的直线交抛物线的对称轴于点D，联结BC，求∠CBD的余切值；

    （3）点P为抛物线上一个动点，当∠PBA=∠CBD时，求点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

    （1）概念理解

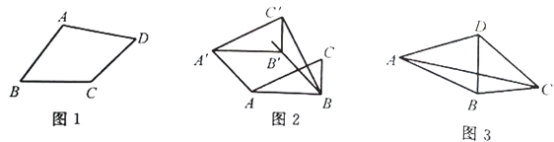
    如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．

    （2）问题探究

    ①小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由．

    ②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB＇方向平移得到△A＇B＇C＇，连结AA＇，BC＇．小红要是平移后的四边形ABC＇A＇是“等邻边四边形”，应平移多少距离（即线段BB＇的长）？

    （3）应用拓展

    如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD==90°，AC，BD为对角线，AC=AB．试探究BC，CD，BD的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

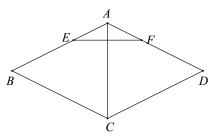
    【题目】如图，在菱形ABCD中，AC为对角线，点E，F分别在AB，AD上，BE=DF，连接EF．

    （1）求证：AC⊥EF；

    （2）延长EF交CD的延长线于点G，连接BD交AC于点O，若BD=4，tanG=，求AO的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，已知AB＞BC．

    （1）实践与操作：作∠ADC的平分线交AB于点E，在DC上截取DF=AD，连接EF；（要求：尺规作图，保留作图痕迹，不写作法）

    （2）猜想并证明：猜想四边形AEFD的形状，并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时，遇到以下问题，请你逐一加以解答：

    （1）如图1，正方形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，则EF　 　GH；（填“＞”“=”或“＜”）

    （2）如图2，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求证： =；

    （3）如图3，四边形ABCD中，∠ABC=∠ADC=90°，BC=3，CD=5，AD=7．5，AM⊥DN，点M，N分别在边BC，AB上，求的值．

    查看答案和解析>>

    同步练习册答案