
����Ŀ��ij�ࡰ�����֡���ѧѧϰ����С��Ծ������������ഹֱ���߶���������ڱߵ�������ϵ����̽��ʱ�������������⣬������һ���Խ��
��1����ͼ1��������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����EF�� ��GH�����������=��������
��2����ͼ2������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����֤��![]() =
=![]() ��
��
��3����ͼ3���ı���ABCD�У���ABC=��ADC=90�㣬BC=3��CD=5��AD=7��5��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���![]() ��ֵ��
��ֵ��

���𰸡���1��=����2������������3��![]()
��������
��1�����ȹ���A��AP��GH����BC��P������B��BQ��EF����CD��Q����BQ��T��Ȼ����������ε������Լ���ABP�ա�BCQ���ж������ʣ����ɵó�EF=GH��
��2�����ȹ���A��AP��EF����CD��P������B��BQ��GH����AD��Q��Ȼ����ݾ��ε������Լ���PDA�ס�QAB���ж������ʣ����ɵó�![]() ��
��
��3�����ȹ���D��ƽ����AB��ֱ�ߣ�������Aƽ����BC��ֱ����R����BC���ӳ�����S���ж�ƽ���ı���ABSR�Ǿ��Σ��ɣ�1�����۵ó�![]() ��Ȼ���ж���ARD�ס�DSC�����������ʺ��ɶ����������̣���⼴��.
��Ȼ���ж���ARD�ס�DSC�����������ʺ��ɶ����������̣���⼴��.
��1����ͼ1�У�����A��AP��GH����BC��P������B��BQ��EF����CD��Q����BQ��T��

���ı���ABCD�������Σ�
��AB��DC��AD��BC��AB=BC����ABP=��C=90��
���ı���BEFQ���ı���PHGA����ƽ���ı��Σ�
��AP=GH��EF=BQ��
�֡�GH��EF��
��AP��BQ��
���PBT+��ABT=90�㣬��ABT+��BAT=90�㣬
���CBQ=��BAT��
�ڡ�ABP�͡�BCQ�У�
 ��
��
���ABP�ա�BCQ��
��AP=BQ��
��EF=GH��
�ʴ�Ϊ��=��
��2������A��AP��EF����CD��P������B��BQ��GH����AD��Q����ͼ2��

���ı���ABCD�Ǿ��Σ�
��AB��DC��AD��BC��
���ı���AEFP���ı���BHGQ����ƽ���ı��Σ�
��AP=EF��GH=BQ��
�֡�GH��EF��
��AP��BQ��
���QAT+��AQT=90�㣬
���ı���ABCD�Ǿ��Σ�
���DAB=��D=90�㣬
���DAP+��DPA=90�㣬
���AQT=��DPA��
���PDA�ס�QAB��
��![]() ��
��
��![]()
![]() ��
��
��3������D��ƽ����AB��ֱ�ߣ�������Aƽ����BC��ֱ����R����BC���ӳ�����S����ͼ3��

���ı���ABSR��ƽ���ı��Σ�
�ߡ�ABC=90�㣬
��ƽ���ı���ABSR�Ǿ��Σ�
���R=��S=90�㣬RS=AB=10��AR=BS��
��AM��DN��
���ɣ�1���еĽ��ۿɵ�![]() ��
��
��SC=x����AR=BS=3+x��
�ߡ�ADC=��R=��S=90�㣬
���ADR+��RAD=90�㣬��ADR+��SDC=90�㣬
���RAD=��CDS��
���ARD�ס�DSC��
��![]() =
=![]() =
=![]() ��
��
��DR=![]() x��DS=
x��DS=![]() ��x+3����
��x+3����
��Rt��ARD����AD2=AR2+DR2��
��7.52=��x+3��2+��![]() x��2��
x��2��
������13x2+24x��189=0�����x=3��![]() ��
��
��AR=6��AB=RS=![]() ��
��
��![]() =
=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ��������һ��̨�Ľ���ͼ����̨CD��ˮƽ�ߵļн�Ϊ30������ʹ�C�����ľ���BCΪ2.5�ף���C��D��ǰ���д�ֱ�ڵ�������EF����C��D���������˶���F�����Ƿֱ�Ϊ60����30����CD��Ϊ10�ף�������ʽ�У������迪ʼ����ʱ������Ҳ�������1.5��P��ͬʱȽȽ���𣬹��貥�Ž���ʱ������պ���������˶���F����֪���貥��ʱ��Ϊ46�룬�����������ƽ���ٶȣ��������ȷ��0.01��/�룩

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y����x2��2x+3��x������ҽ���A��B���㣬��y�ύ�ڵ�C������ΪD

��1����ֱ��AC�Ľ���ʽ���D�����ꣻ
��2����ֱ��AC�Ϸ�������������һ��E����EF��x�ᣬ�������߽��ڵ�F����EM��x����M����FN��x����N������Ϊ2![]() ���߶�PQ��ֱ��AC���˶�����P�ڵ�Q�Ҳࣩ�����ı���EMNF���ܳ�ȡ���ֵ���ı���DPQE���ܳ�����Сֵ����Ӧ�ĵ�Q�����ꣻ
���߶�PQ��ֱ��AC���˶�����P�ڵ�Q�Ҳࣩ�����ı���EMNF���ܳ�ȡ���ֵ���ı���DPQE���ܳ�����Сֵ����Ӧ�ĵ�Q�����ꣻ
��3����ͼ2��ƽ�������ߣ�ʹ�����ߵĶ���D��ֱ��AD���ƶ�����Dƽ�ƺ�Ķ�Ӧ��ΪD������Aƽ�ƺ�Ķ�Ӧ��ΪA������A��D��C�Ƿ���Ϊֱ�������Σ����ܣ��������Ӧ���߶�D��C�ij��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУУ���γ�����Ϊ�˽��Уѧ��ϲ��У���γ̵��������ȡ��������İ취��ͨ���鷨�����ա����ա��������ſγ̵�ѡ���������������ѧ������Ȥ���ã�Ҫ��ÿλͬѧֻ��ѡ��һ���Լ�ϲ���Ŀγ̣��������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺
��1������ε����о��У�һ���������� ����ѧ����ϲ�����յ�����������ͳ��ͼ����ռ��Բ�Ľ����� ���ȣ�
��2���벹ȫƵ���ֲ�����ͳ��ͼ��
��3��Ϊ��ƽ���У���γ̵���������Ҫ��ϲ�����տγ̵ļס��ҡ���3���е���2�˵����տγ̣������б�����״ͼ�ķ����ס������˱�ͬʱ���������տγ̡��ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A1��A2��A3������An��y����������ϣ���B1��B2��B3������Bn�ڶ��κ���y=x2λ�ڵ�һ����ͼ���ϣ�����OB1A1����A1B2A2����A2B3A3��������An-1BnAn���ǵ���ֱ�������Σ����С�B1=��B2=��B3=��=��Bn=90������B1������Ϊ______���߶�A1A2�ij�Ϊ______����An-1BnAn�����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
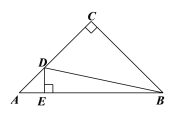
����Ŀ���Ķ����⣺��ͼ��Rt��AB�У�![]() ��AC=BC��AB= 4cm������D����A��C��B�ķ����A���˶���B�㣮DE
��AC=BC��AB= 4cm������D����A��C��B�ķ����A���˶���B�㣮DE![]() AB������ΪE����AE��Ϊ
AB������ΪE����AE��Ϊ![]() cm��BD��Ϊ
cm��BD��Ϊ![]() cm����D��A�� ��ʱ��
cm����D��A�� ��ʱ��![]() = 4����D��B�غ�ʱ
= 4����D��B�غ�ʱ![]() =0����С�Ƹ���ѧϰ�����ľ��飬�Ժ���
=0����С�Ƹ���ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����������С�Ƶ�̽�����̣��벹��������
�ı仯���仯�Ĺ��ɽ�����̽����������С�Ƶ�̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 4 | 3.5 | 3.2 |
| 2.8 | 2.1 | 1.4 | 0.7 | 0 |
��ȫ�������Ҫ��������һλС������![]() __________��
__________��
��2��������������н���ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺��DB=AEʱ��AE�ij���ԼΪ�� �� cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
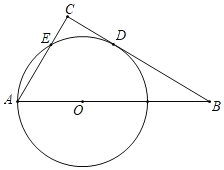
����Ŀ����ͼ����֪Rt��ABC�У�CAB=60�㣬��OΪб��AB��һ�㣬��OA=2����OAΪ�뾶����O��BC������D����AC���ڵ�E������AD��
��1�����߶�CD�ij���
��2������O��Rt��ABC�ص����ֵ���������������ȷֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����F������ABCD�Ķ���A��������A��D��B��1cm/s���ٶ������˶�����B��ͼ2�ǵ�F�˶�ʱ����FBC�����y��cm2����ʱ��x��s���仯�Ĺ�ϵͼ����a��ֵΪ��������

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com