
����Ŀ���Ķ����⣺��ͼ��Rt��AB�У�![]() ��AC=BC��AB= 4cm������D����A��C��B�ķ����A���˶���B�㣮DE
��AC=BC��AB= 4cm������D����A��C��B�ķ����A���˶���B�㣮DE![]() AB������ΪE����AE��Ϊ
AB������ΪE����AE��Ϊ![]() cm��BD��Ϊ
cm��BD��Ϊ![]() cm����D��A�� ��ʱ��
cm����D��A�� ��ʱ��![]() = 4����D��B�غ�ʱ
= 4����D��B�غ�ʱ![]() =0����С�Ƹ���ѧϰ�����ľ��飬�Ժ���
=0����С�Ƹ���ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����������С�Ƶ�̽�����̣��벹��������
�ı仯���仯�Ĺ��ɽ�����̽����������С�Ƶ�̽�����̣��벹��������
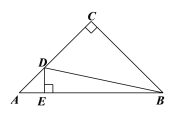
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 4 | 3.5 | 3.2 |
| 2.8 | 2.1 | 1.4 | 0.7 | 0 |
��ȫ�������Ҫ��������һλС������![]() __________��
__________��
��2��������������н���ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺��DB=AEʱ��AE�ij���ԼΪ�� �� cm��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
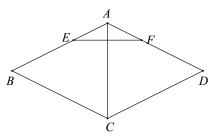
����Ŀ����ͼ��������ABCD�У�ACΪ�Խ��ߣ���E��F�ֱ���AB��AD�ϣ�BE=DF������EF��
��1����֤��AC��EF��
��2���ӳ�EF��CD���ӳ����ڵ�G������BD��AC�ڵ�O����BD=4��tanG=![]() ����AO�ij���
����AO�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�����ó�![]() �����Χ��һ�������ε���������С�ã�������һ�濿�ڳ�Ϊ
�����Χ��һ�������ε���������С�ã�������һ�濿�ڳ�Ϊ![]() ��ǽ�ϣ���ͼ����
��ǽ�ϣ���ͼ����

��1�������������Ϊ![]() ƽ���ף��������ij��Ϳ���
ƽ���ף��������ij��Ϳ���
��2���ܷ�Χ�����Ϊ![]() ƽ�������������ܣ�������Ϳ��������ܣ���˵�����ɣ�
ƽ�������������ܣ�������Ϳ��������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ࡰ�����֡���ѧѧϰ����С��Ծ������������ഹֱ���߶���������ڱߵ�������ϵ����̽��ʱ�������������⣬������һ���Խ��
��1����ͼ1��������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����EF�� ��GH�����������=��������
��2����ͼ2������ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H����֤��![]() =
=![]() ��
��
��3����ͼ3���ı���ABCD�У���ABC=��ADC=90�㣬BC=3��CD=5��AD=7��5��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�ı�AB��ADΪ�ױ߷ֱ�������������ABE�͵���������ADF.
��1�����ı���ABCDΪ������ʱ����ͼ�٣����Ա�AB��ADΪб�߷ֱ������������ֱ����ABE�͵���ֱ����ADF������BF��ED���߶�BF��ED��������ϵ��_____________��
��2�����ı���ABCDΪ����ʱ����ͼ�ڣ����Ա�AB��ADΪб�߷ֱ�������ڲࡢ���������ֱ����ABE�͵���ֱ����ADF������EF��BD���߶�EF��BD����������������ϵ����˵�����ɣ�
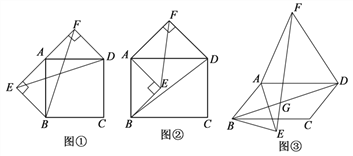
��3�����ı���ABCDΪƽ���ı���ʱ���Ա�AB��ADΪ�ױ߷ֱ���ƽ���ı����ڲࡢ�����������ABE�͵�����ADF������ABE����ADF�Ķ��Ǿ�Ϊ![]() ������EF��BD������ΪG.����
������EF��BD������ΪG.����![]() ��ʾ����FGD����˵������.
��ʾ����FGD����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
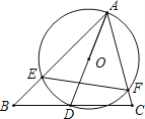
����Ŀ����ͼ����ABC�У���BAC=60������ABC=45����AB=2![]() ��D���߶�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC��E��F������EF�����߶�EF���ȵ���СֵΪ______��
��D���߶�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC��E��F������EF�����߶�EF���ȵ���СֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=��x+7a+1��ֱ��y=2x��2a+4ͬʱ������P����Q����M��0����1��ΪԲ�ģ�MOΪ�뾶��Բ�ϵ�һ�����㣬���߶�PQ����СֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У���
�У���![]() �ڶԽ���
�ڶԽ���![]() �ϣ���
�ϣ���![]() �ڱ�
�ڱ�![]() �ϣ�����
�ϣ�����![]() ��
��![]() ��
��![]() ���Խ���
���Խ���![]() �ڵ�
�ڵ�![]() ����
����![]() .
.
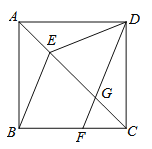
��1����֤��![]() ��
��
��2�����ж�![]() ��
��![]() ��λ�ù�ϵ����˵������.
��λ�ù�ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
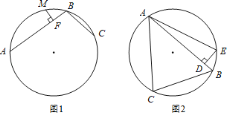
����Ŀ�����壺Բ���й����˵����������ɵ����߳�ΪԲ��һ�����ң����������Ҷ�������ͼ1��AB��BC���Բ�����ң�AB��BC��M�ǻ�ABC���е㣬MF��AB��F����AF��FB+BC��
��ͼ2����ABC�У���ABC��60�㣬AB��8��BC��6��D��AB��һ�㣬BD��1����DE��AB����ABC�����Բ��E������EA�����EAC��_____�㣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com