
【题目】如图,![]() 给出下列结论:①
给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有_______(填写答案序号).
.其中正确的有_______(填写答案序号).

【答案】①③④
【解析】
利用AAS可证明△ABE≌△ACF,可得AC=AB,∠BAE=∠CAF,利用角的和差关系可得∠EAM=∠FAN,可得③正确,利用ASA可证明△AEM≌△AFN,可得EM=FN,AM=AN,可得①③正确;根据线段的和差关系可得CM=BN,利用AAS可证明△CDM≌△BDN,可得CD=DB,可得②错误;利用ASA可证明△ACN≌△ABM,可得④正确;综上即可得答案.
在△ABE和△ACF中,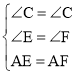 ,
,
∴△ABE≌△ACF,
∴AB=AC,∠BAE=∠CAF,
∴∠BAE-∠BAC=∠CAF-∠BAC,即∠FAN=∠EAM,故③正确,
在△AEM和△AFN中,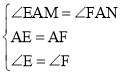 ,
,
∴△AEM≌△AFN,
∴EM=FN,AM=AN,故①正确,
∴AC-AM=AB-AN,即CM=BN,
在△CDM和△BDN中,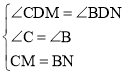 ,
,
∴CD=DB,故②错误,
在△CAN和△ABM中,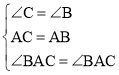 ,
,
∴△ACN≌△ABM,故④正确,
综上所述:正确的结论有①③④,
故答案为:①③④


科目:初中数学 来源: 题型:
【题目】将下表从左到右在毎个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2017个格子中的数字是( )
3 |
|
|
| -1 | 2 | …… |
A.3B.2C.0D.-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
(应用)请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
(拓展)计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒1cm,设运动的时间为x秒.
的路径运动,且速度为每秒1cm,设运动的时间为x秒.
(1)当x=__ __秒 时,CP把△ABC的面积分成相等的两部分,并求出此时CP=__ __cm;
(2)当x为何值时,△ABP为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
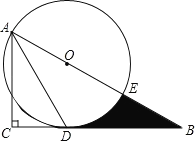
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从锦江区社保局获悉,我区范围内已经实现了全员城乡居民新型社会合作医疗保险制度.享受医保的城乡居民可在规定的医院就医并按规定标准报销部分医疗费用.下表是住院费用报销的标准:
住院费用x(元) | 0<x<5000 | 5000<x≤20000 | x>20000 |
每年报销比例 | 40% | 50% | 60% |
(说明:住院费用的报销采取分段计算方式,如:某人一年住院费用共30000元,则5000元按40%报销,15000元按50%报销,余下的10000元按60%报销;实际支付的住院费=住院费用-按标准报销的金额.)
(1)若我区居民张大哥一年住院费用为20000元,则按标准报销的金额为 元,张大哥实际支付了 元的住院费;
(2)若我区居民王大爷一年内本人实际支付的住院费用为21000元,则王大爷当年的住院费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
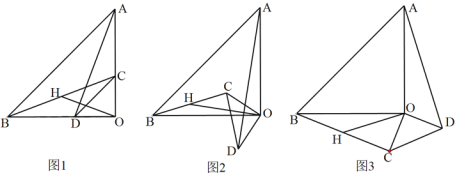
(1)如图1所示,求证:![]() 且
且![]()
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com