正方形的性质：正方形具有四边形、平行四边形、矩形、菱形的一切性质，正方形的四个角都______；四条边都______且__________________；正方形的两条对角线______，并且互相______，每条对角线平分______对角．它有______条对称轴．
心算口算巧算一课一练系列答案科目：初中数学 来源： 题型：
某市要在一块□ABCD的空地上建造一个四边形花园，要求花园所占面积是□ABCD面积的一半，并且四边形花园的四个顶点作为出入口，要求分别在□ABCD的四条边上，请你设计两种方案：
方案(1)：如图1所示，两个出入口E、F已确定，请在图1上画出符合要求的四边形花园，并简要说明画法；
图1
方案(2)：如图2所示，一个出入口M已确定，请在图2上画出符合要求的梯形花园，并简要说明画法．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连结DP交AC于点Q．
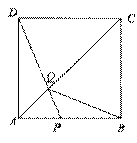
(1)试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
(2)当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的
；
(3)若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，□ABCD中，AB⊥AC，AB＝1，BC＝
．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．
(1)证明：当旋转角为90°时，四边形ABEF是平行四边形；
(2)试说明在旋转过程中，线段AF与EC总保持相等；
(3)在旋转过程中，四边形BEDF可能是菱形吗?如果不能，请说明理由；如果能，画出图形并写出此时AC绕点O顺时针旋转的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列命题中，正确的是( )．
(A)两邻边相等的四边形是菱形
(B)一条对角线平分一个内角的平行四边形是菱形
(C)对角线垂直且一组邻边相等的四边形是菱形
(D)对角线垂直的四边形是菱形
查看答案和解析>>
科目：初中数学 来源： 题型：
能判定四边形ABCD是平行四边形的条件是：∠A∶∠B∶∠C∶∠D的值为( )．
(A)1∶2∶3∶4 (B)1∶4∶2∶3
(C)1∶2∶2∶1 (D)1∶2∶1∶2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
求
．(精确到0.01)
，那么EF＋EG的长为______．