
已知,AB为⊙O的直径,C为⊙O上一点,若直线CD与⊙O相切于点C,AD⊥CD,垂足为D.
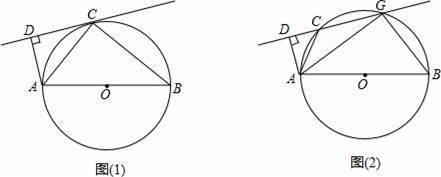

(1)如图①,AB=10,AD=2,求AC的长;
(2)如果把直线CD向下平行移动,如图(2),直线CD交⊙O于C,G两点,若题目中的其他条件不变,且AG=4,BG=3,求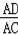
 的值.
的值.
【考点】切线的性质;平移的性质.
【分析】(1)先由圆周角定理得出∠ACB=90°=∠ADC,再由弦切角定理得出∠ACD=∠B,证出△ACD∽△ABC,得出对应边成比例,得出AC2=AB•AD,即可求出AC;
(2)先根据勾股定理求出AB,再由圆内接四边形的性质得出∠ACD=∠B,证出△ACD∽△ABC,得出比例式即可得出结果.
【解答】解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵直线CD与⊙O相切于点C,
∴∠ACD=∠B,
又∵AD⊥CD,
∴∠CDA=90°=∠ACB,
∴△ACD∽△ABC,
∴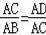
 ,
,
∴AC2=AB•AD=10×2=20,
∴AC=2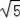
 ;
;
(2)∵AB为⊙O的直径,
∴∠AGB=90°,
∴AB=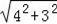
 =5,
=5,
∵AD⊥CD,
∴∠CDA=90°=∠AGB,
又∵∠ACD=∠B,
∴△ACD∽△ABC,
∴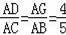
 .
.
【点评】本题考查了切线的性质、弦切角定理、圆周角定理、勾股定理、相似三角形的判定与性质;熟练掌握圆的有关定理,证明三角形相似是解决问题的关键.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
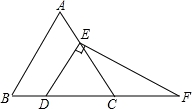
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
|
| 甲 | 乙 | 丙 | 丁 |
| 平均数 | 80 | 85 | 85 | 80 |
| 方 差 | 42 | 42 | 54 | 59 |
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
八月份利川市政府计划在总费用2300元的限额内,租用汽车送234名运动员和6名教练到恩施州参加第二届全州青少年运动会,每辆汽车上至少要有1名教练.现有甲、乙两种大客车,它们的载客量和租金如下表:
|
| 甲种客车 | 乙种客车 |
| 载客量/(人/辆) | 45 | 30 |
| 租金/(元/辆) | 400 | 280 |
(1)共需租多少辆汽车?
(2)有几种租车方案?
(3)最节省费用的是哪种租车方案?.
查看答案和解析>>
科目:初中数学 来源: 题型:
某中学七年级学生共450人,其中男生250人,女生200人,该样对七年级所有学一进生了一次体育测试,并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表.
(1) 请解释“随机抽取了50名男生和
40名女生”的合理性;
(2) 从上表的“频数”、“百分比”两
列数据中选择一列,用适当的统计图表示;
估计该校七年级学生体育测试成绩不及格
的人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com