
分析 先画图,由对顶角和题意可得∠PEA=∠PEB=∠CED=∠AED=60°,即可求∠PCA,∠PBE,∠ABD,∠BAD,∠PAE的值,由∠PAC=∠PAE+∠CAE即可得解.
解答 解:如图所示: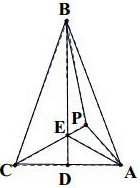
由题意可得:∠PEA=∠PEB=∠CED=∠AED,
而∠PEA+∠PEB+AED=180°,
所以∠PEA=∠PEB=∠CED=∠AED=60°,
所以可得∠PCA=30°,
又∠BPC=108°,所以∠PBE=12°,从而∠ABD=24°,
所以∠BAD=90°-24°=66°,
所以∠PAE=$\frac{1}{2}$(∠BAD-∠CAE)=$\frac{1}{2}$(66°-30°)=18°,
所以∠PAC=∠PAE+∠CAE=18°+30°=48°.
故答案为:48°.
点评 本题主要考查了等腰三角形的性质,三角形内心,三角形内角和等知识的应用,考查了分析问题解决问题的能力,考查了转化思想,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
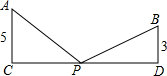 如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?
如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
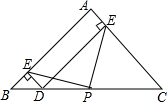 如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.
如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
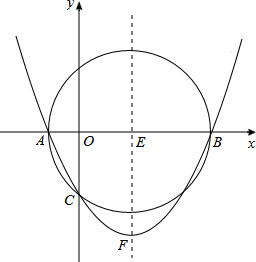 如图,已知以E(6,0)为圆心,以10为半径的⊙E与x轴交于A.B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F;
如图,已知以E(6,0)为圆心,以10为半径的⊙E与x轴交于A.B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com