
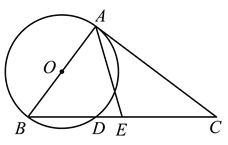
【题目】如图,以AB为直径作⊙O,过点A作⊙O的切线AC,连结BC,交⊙O于点D,点E是BC边的中点,连结AE.
(1)求证:∠AEB=2∠C;
(2)若AB=6,![]() ,求DE的长.
,求DE的长.
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)由AC是⊙O的切线,得出∠BAC=90°.再利用直角三角形斜边中线定理、等腰三角形的性质、三角形的外角即可证出结论;
(2)连结AD,由圆周角定理的推论可得出∠ABD=90°.然后利用锐角三角函数即可得出答案.
详解:(1)证明:∵AC是⊙O的切线,
∴∠BAC=90°,
∵点E是BC边的中点,
∴AE=EC,
∴∠C=∠EAC,
∵∠AEB=∠C+∠EAC,
∴∠AEB=2∠C.
(2)解:连结AD.

∵AB为直径作⊙O,
∴∠ABD=90°,
∵AB=6,![]() ,
,
∴BD=![]() ,
,
在Rt△ABC中,AB=6,![]() ,
,
∴BC=10,
∵点E是BC边的中点,
∴BE=5,
∴![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,点D是线段AB上的任意一点(不与点A和B重合),C是线段AD的中点,AB=4cm.
![]()
(1)若D是线段AB的中点,求线段CD的长度.
(2)在图中作线段DB的中点E,当点D在线段AB上从左向右移动时,试探究线段CE长度的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() |,
|,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:(1)因为![]() ,所以
,所以![]() ______;
______;
因为![]() ,所以
,所以![]() ______;
______;
又因为![]() ,
,
所以当![]() ______时,
______时,![]() ______;
______;
或当![]() ______时,
______时,![]() ______,
______,
∴![]() ______或_______.
______或_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表所示是2019年元月的月历表.下列结论:
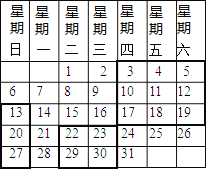
①每一竖列上相邻的两个数,下面的数比上面的数大7;
②可以框出一竖列上相邻的三个数(如图所示),这三个数的和是24;
③不可以框出一个2×2的矩形块的四个数(如图所示),这四个数的和是82;
④任意框出一个3×3的矩形块的九个数(如图所示),这九个数的和是中间数的9倍,其中正确的是_____(把所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
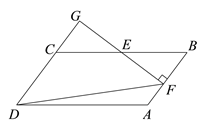
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2bx﹣3的对称轴为直线x=2.
(1)求b的值;
(2)在y轴上有一动点P(0,m),过点P作垂直y轴的直线交抛物线于点A(x1,y1),B(x2,y2),其中x1<x2.
①当x2﹣x1=3时,结合函数图象,求出m的值;
②把直线PB下方的函数图象,沿直线PB向上翻折,图象的其余部分保持不变,得到一个新的图象W,新图象W在0≤x≤5时,﹣4≤y≤4,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五四”青年节期间,校团委对团员参加活动情况进行表彰,计划分为优秀奖和贡献奖,为此联系印刷公司设计了两种奖状,A,B两家公司都为学校提出了相同规格和单价的两种奖状,其中优秀奖的奖状6元/张,贡献奖的奖状5元/张,经过协商,A公司的优惠条件是:两种奖状都打八折,但要收制版费50元;B公司的优惠条件是:两种奖状都打九折;根据学校要求,优秀奖的个数是贡献奖的2倍还多10个,如果设贡献奖的个数是x个.
(1)分别写出校团委购买A,B两家印刷厂所需要的总费用y1(元)和y2(元)与贡献奖个数x之间的函数关系式;
(2)校团委选择哪家印刷公司比较合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() ,在不再连接其他线段的前提下,要使四边形
,在不再连接其他线段的前提下,要使四边形![]() 成为菱形,还需添加一个条件,这个条件不可能是( )
成为菱形,还需添加一个条件,这个条件不可能是( )
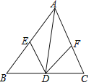
A. BD=DC B. AB=AC
C. AD=BC D. AD⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得:
,得:![]() ,
,![]() ;
;
(2)利用所探索的结论,找一组正整数![]() 、
、![]() 、
、![]() 、
、![]() 填空:
填空: ![]()
![]()
![]()
![]()
![]() ;
;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com