
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在图中正确作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 ,△A′B′C′的面积为 .

科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作试验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组线段的长为边,能组成三角形的是( )
A.3cm,6cm,8cmB.3cm,2cm,6cmC.5cm,6cm,11cmD.2cm,7cm,4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
学习了三角形全等的判定方法(即“SSS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
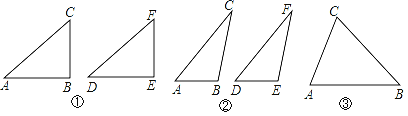
如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,请你证明:△ABC≌△DEF(提示:过点C作CG⊥AB交AB的延长线于G,过点F作FH⊥DE交DE的延长线于H).
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你利用图③,在图③中用尺规作出△DEF,使△DEF和△ABC不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个商店把iPad按标价的九折出售,仍可获利20%,若该iPad的进价是2400元,则ipad标价是( )
A.3200元
B.3429元
C.2667元
D.3168元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将A(1,1)先向左平移2个单位,再向下平移2个单位得点B,则点B的坐标是( )
A.(-1,-1)B.(3,3)C.(0,0)D.(-1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图1,在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
小红提出了一个猜想:对角线互相平分且相等的“等邻边四边形”是正方形.她的猜想正确吗?请说明理由.
(3)如图2,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC=![]() AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.
AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com