
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图1,在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
小红提出了一个猜想:对角线互相平分且相等的“等邻边四边形”是正方形.她的猜想正确吗?请说明理由.
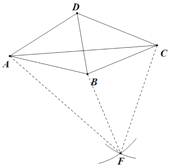
(3)如图2,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC=![]() AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.
AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.


【答案】(1)AB=BC,(答案不唯一),理由见解析;(2)正确;理由见解析;(3)BC2+CD2=2BD2,证明见解析.
【解析】试题分析:(1)利用“等邻边四边形”的定义直接判断即可,
(2)利用矩形的判定和菱形的判定和“等邻边四边形”的定义直接判断即可,
(3)先判断出△ACF∽△ABD,得到CF=![]() BD,再求出∠CBF=90°,最后用勾股定理即可求解.
BD,再求出∠CBF=90°,最后用勾股定理即可求解.
试题解析:(1)AB=BC,(答案不唯一)
理由:∵四边形ABCD是凸四边形,且AB=AC,
∴四边形ABCD是“等邻边四边形”.
(2)正确;理由为:
∵四边形的对角线互相平分且相等,
∴四边形ABCD是矩形 ,
∵四边形是“等邻边四边形”,
∴这个四边形有一组邻边相等,
∴四边形ABCD是菱形 ,
∴对角线互相平分且相等的等邻边四边形是正方形;
(3)BC2+CD2=2BD2,证明如下:
如图,
∵AB=AD,
∴以A为圆心,AC为半径画弧,再以B为圆心,CD为半径画弧,两弧相交于点F
则可将△ADC线绕点A旋转到△ABF,连接CF,
则△ABF≌△ADC,
∴∠ABF=∠ADC,∠BAF=∠DAC,AF=AC,FB=CD,
∴∠BAD=∠CAF, ![]() ,
,
∴△ACF∽△ABD,
∴![]() ,
,
∵AC=![]() AB,∴CF=
AB,∴CF=![]() BD,
BD,
∵∠BAD+∠ADC+∠BCD+∠ABC=360°,
∴∠ABC+∠ADC=360°-(∠BAD+∠BCD)=360°-90°=270°,
∴∠ABC+∠ABF=270°,
∴∠CBF=90°,
∴BC2+FB2=CF2=(![]() BD)2=2BD2,
BD)2=2BD2,
∴BC2+CD2=2BD2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在图中正确作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)点B′的坐标为 ,△A′B′C′的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为方便顾客停车,决定设计一个地下停车场,为了测得该校地下停车场的限高CD,在施工时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
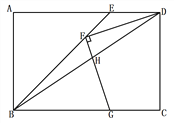
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD = FG, ![]() ,BG = 4,则GH的长为__________.
,BG = 4,则GH的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个如图示的长方体的透明玻璃杯,其长AD=8cm,高AB=6cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=6cm,一小虫想从杯外的A处沿壁爬进杯内的G处吃掉食物.
(1)小虫应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.
(2)求小虫爬行的最短路线长(不计杯壁厚度).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com