
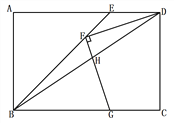
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD = FG, ![]() ,BG = 4,则GH的长为__________.
,BG = 4,则GH的长为__________.
【答案】![]()
【解析】过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,过点A作AP⊥BD于点P,延长DF交AB于点K,过点K作KQ⊥BD于点Q,如图所示。

∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中,
 ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM,NF=MG.
∵∠BAD=90°,BE平分∠ABC,
∴∠ABE=∠CBE=45°,
又∵FM⊥BM,
∴FM=BM,
∵BF=![]() ,
,
∴BM=FM=3,MG=BGBM=43=1,
∴NF=MG=1,AB=NM=4,AD=AN+ND=BM+FM=6,
∴BD=![]() .
.
由面积公式可知:S△ABD=![]() BDAP=
BDAP=![]() ABAD,即
ABAD,即![]() AP=4×6,
AP=4×6,
∴AP=![]() ,
,
∵NF∥AB,
∴△DNF∽△DAK,
∴![]() ,
,
∴AK=2NF=2,DK= ![]() =2
=2![]() ,DF=
,DF=![]() =
=![]() .
.
∴BK=ABAK=42=2,
∵KQ∥AP,
∴△BKQ∽△BAP,
∴![]() ,即,
,即,  ,
,
∴KQ=![]() ,
,
∴BQ=![]() =
= =
=![]() ,
,
∴DQ=BDBQ=![]()
![]() =
=![]() ,
,
∵∠DFH=∠DQK=90°,∠FDH=∠QDK,
∴△DFH∽△DQK,
∴![]() ,
,
即 ,
,
∴FH=![]() ,
,
∴GH=FGFH=![]()
![]() =
=![]() .
.
故答案为: ![]()


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图1,在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
小红提出了一个猜想:对角线互相平分且相等的“等邻边四边形”是正方形.她的猜想正确吗?请说明理由.
(3)如图2,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC=![]() AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.
AB.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若多项式3x2﹣2xy﹣y2减去多项式M所得的差是﹣5x2+xy﹣2y2 , 则多项式M是( )
A.﹣2x2﹣xy﹣3y2
B.2x2+xy+3y2
C.8x2﹣3xy+y2
D.﹣8x2+3xy﹣y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于y轴对称,那么(m+n)2016的值为( )
A. ﹣1 B. 1 C. ﹣72016 D. 72016
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com