
【题目】如图,已知直线AC∥BD,直线AB,CD不平行,点P在直线AB上,且和点A、B不重合.

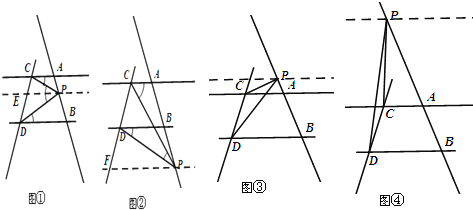
(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)当点P在A、B两点之间运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
(3)如图②,当点P在线段AB延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?并说明理由.
(4)当点P在线段BA延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
【答案】(1)50°;(2)∠CPD=∠PCA+∠PDB;(3)∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB;(4)见解析
【解析】
试题分析:(1)如图①,过P点作PE∥AC交CD于E点,由于AC∥BD,则PE∥BD,根据平行线的性质得∠CPE=∠PCA=20°,∠DPE=∠PDB=30°,所以∠CPD=50°;
(2)证明方法与(1)一样;
(3)如图②,过P点作PF∥BD交CD于F点,由于AC∥BD,则PF∥AC,根据平行线的性质得∠CPF=∠PCA,∠DPF=∠PDB,所以∠CPD=∠PCA﹣∠PDB;
(4)如图③和④,类似(3)的说明方法易得∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系.
解:(1)如图①,过P点作PE∥AC交CD于E点,
∵AC∥BD
∴PE∥BD,
∴∠CPE=∠PCA=20°,∠DPE=∠PDB=30°,
∴∠CPD=∠CPE+∠DPE=50°;
(2)∠CPD=∠PCA+∠PDB(证明方法与(1)一样;
(3)∠CPD=∠PCA﹣∠PDB.理由如下:
如图②,过P点作PF∥BD交CD于F点,
∵AC∥BD,
∴PF∥AC,
∴∠CPF=∠PCA,∠DPF=∠PDB,
∴∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB;
(4)如图③,∠CPD=∠PDB﹣∠PCA;
如图④,∠CPD=∠PCA﹣∠PDB.
(证明方法与(3)类似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.

(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 两条对角线相等的四边形是矩形
B. 两条对角线互相垂直且平分的四边形是正方形
C. 等边三角形既是轴对称图形又是中心对称图形
D. 有一个角是60°的等腰三角形是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
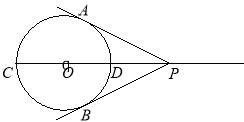
(1)、连接![]() ,若
,若![]() ,试证明
,试证明![]() 是等腰三角形;
是等腰三角形;
(2)、填空:①当![]() =
= ![]() 时,四边形
时,四边形![]() 是菱形;②当
是菱形;②当![]() =
= ![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是真命题的是( )
A. 如果a>0,b>0,则a+b>0
B. 直角都相等
C. 两直线平行,同位角相等
D. 若a=6,则|a|=|6|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com