Question

【题目】如图（1），在矩形ABCD中，AB=3，BC=4，连接BD．现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上，一条直角边过点C，另一条直角边与AB所在的直线交于点G．

（1）是否存在这样的点P，使点P、C、G为顶点的三角形与△GCB全等？若存在，画出图形，并直接在图形下方写出BG的长．（如果你有多种情况，请用①、②、③、…表示，每种情况用一个图形单独表示，如果图形不够用，请自己画图）

（2）如图（2），当点P在BD的延长线上时，以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F，连EF，分别过点G、C作GM⊥EF，CN⊥EF，M、N为垂足．试探究PM与FN的关系．

Answer 1

【答案】（1）BG=3；见解析（2）PM=FN．

【解析】

试题分析：（1）只需分点G在线段AB上（如图①）、在线段AB的延长线上（如图②）、在线段AB的反向延长线上（如图③）三种情况讨论，即可解决问题；

（2）如图2，由（1）可知，此时BG=PG=，BC=PC=4．易证△PGM∽△CPN，从而可得PM=CN；易证△FNC∽△BCD，从而可得FN=CN，即可得到PM=FN．

解：（1）存在点P，使点P、C、G为顶点的三角形与△GCB全等．

①若点G在线段AB上，如图①．

当BG=PC时，根据HL可得Rt△GBC≌Rt△CPG，

此时∠GCB=∠CGP，

∴PG∥BC，

∴∠GPC+∠PCB=90°．

∵∠GPC=90°，

∴∠PCB=90°，

∴点P在点D处，

∴BG=PC=DC=AB=3；

②若点G在线段AB的延长线上，如图②．

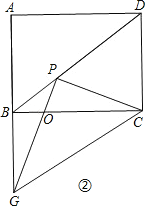
当BG=PC时，根据HL可得Rt△GBC≌Rt△CPG，

此时BC=PG，∠GCB=∠CGP，

∴OG=OC，OB=OP，

∴∠PBO=∠BPO=（180°﹣∠BOP），

∠OCG=∠OGC=（180°﹣∠GOC）．

∵∠BOP=∠GOC，

∴∠PBO=∠OCG，

∴BD∥CG．

∵四边形ABCD是矩形，

∴AB∥DC，即BG∥DC，

∴四边形BGCD是平行四边形，

∴BG=CD=3；

③若点G在线段AB的反向延长线上，如图③．

当PC=BC时，根据HL可得Rt△GBC≌Rt△GPC，

此时BG=PG，

∴点G、C在BP的垂直平分线上，

∴GC垂直平分BP，

∴∠BGC+∠GBD=90°．

∵∠CBD+∠GBD=90°，

∴∠BGC=∠CBD．

又∵∠GBC=∠BCD=90°，

∴△GCB∽△BDC，

∴=．

∵BC=4，CD=3，

∴=，

∴BG=；

（2）如图2，

由（1）可知，此时△GBC≌△GPC，且BG=PG=，BC=PC=4．

∵GM⊥EF，CN⊥EF，

∴∠GMP=∠PNC=90°，

∴∠MGP+∠GPM=90°．

∵∠GPC=90°，

∴∠GPM+∠NPC=90°，

∴∠MGP=∠NPC，

∴△PGM∽△CPN，

∴=．

∴==，即PM=CN．

∵PB=PF，∴∠F=∠PBC．

又∵∠FNC=∠BCD=90°，

∴△FNC∽△BCD，

∴=．

∵BC=4，DC=3，

∴=，

∴FN=CN，

∴PM=FN．